CodeForces

B. Lemmings

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

As you know, lemmings like jumping. For the next spectacular group jump n lemmings gathered near a high rock with k comfortable ledges on it. The first ledge is situated at the height of h meters, the second one is at the height of 2h meters, and so on (the i-th ledge is at the height of i·h meters). The lemmings are going to jump at sunset, and there's not much time left.

Each lemming is characterized by its climbing speed of vi meters per minute and its weight mi. This means that the i-th lemming can climb to the j-th ledge in 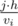 minutes.

To make the jump beautiful, heavier lemmings should jump from higher ledges: if a lemming of weight mi jumps from ledge i, and a lemming of weight mj jumps from ledge j (for i < j), then the inequation mi ≤ mj should be fulfilled.

Since there are n lemmings and only k ledges (k ≤ n), the k lemmings that will take part in the jump need to be chosen. The chosen lemmings should be distributed on the ledges from 1 to k, one lemming per ledge. The lemmings are to be arranged in the order of non-decreasing weight with the increasing height of the ledge. In addition, each lemming should have enough time to get to his ledge, that is, the time of his climb should not exceed t minutes. The lemmings climb to their ledges all at the same time and they do not interfere with each other.

Find the way to arrange the lemmings' jump so that time t is minimized.

Input

The first line contains space-separated integers n, k and h (1 ≤ k ≤ n ≤ 105, 1 ≤ h ≤ 104) — the total number of lemmings, the number of ledges and the distance between adjacent ledges.

The second line contains n space-separated integers m1, m2, ..., mn (1 ≤ mi ≤ 109), where mi is the weight of i-th lemming.

The third line contains n space-separated integers v1, v2, ..., vn (1 ≤ vi ≤ 109), where vi is the speed of i-th lemming.

Output

Print k different numbers from 1 to n — the numbers of the lemmings who go to ledges at heights h, 2h, ..., kh, correspondingly, if the jump is organized in an optimal way. If there are multiple ways to select the lemmings, pick any of them.

Examples

input

5 3 2
1 2 3 2 1
1 2 1 2 10

output

5 2 4

input

5 3 10
3 4 3 2 1
5 4 3 2 1

output

4 3 1

Note

Let's consider the first sample case. The fifth lemming (speed 10) gets to the ledge at height 2 in  minutes; the second lemming (speed 2) gets to the ledge at height 4 in 2 minutes; the fourth lemming (speed 2) gets to the ledge at height 6 in 3 minutes. All lemmings manage to occupy their positions in 3 minutes.

题目链接 

题意 

n个袋鼠要跳k个楼梯，第i个楼梯的高度为i*h。每个袋鼠都有一个速度v和体重m，假如mi<=mj，那么j袋鼠必须跳比i袋鼠更高的楼梯。选出k个袋鼠，问所有袋鼠跳楼梯完成的最短时间是多少？按顺序输出选择袋鼠的序号。

分析 

求最短时间，若我们将v以第一关键字，m以第二关键字，从小到大进行排序，那么我们就可以二分时间了。如何检测当前时间是大了还是小了呢，因为限定了k个楼梯，所以按排序结果从后面依次计算每个袋鼠能跳的阶数，若存在k个或以上的袋鼠符合要求，则说明时间够了或者是多了。

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<algorithm>
#include<cstring>
#include <queue>
#include <vector>
#include<bitset>
#include<map>
using namespace std;
typedef long long LL;
const int maxn = 1e5+5;
const int mod = 772002+233;
typedef pair<int,int> pii;
#define X first
#define Y second
#define pb push_back
#define mp make_pair
#define ms(a,b) memset(a,b,sizeof(a))
const int inf = 0x3f3f3f3f;
#define lson l,m,2*rt
#define rson m+1,r,2*rt+1

struct node{
    int m,v,pos;
    bool operator < (const node&rhs)const{
        if(m!=rhs.m) return m<rhs.m;
        return v<rhs.v;
    }
}d[maxn];
int ans[maxn];
int n,k,h;
int main(){
    scanf("%d%d%d",&n,&k,&h);
    for(int i=1;i<=n;i++) scanf("%d",&d[i].m),d[i].pos=i;
    for(int i=1;i<=n;i++) scanf("%d",&d[i].v);
    sort(d+1,d+1+n);
    double l=0,r=1e9;
    for(int i=0;i<100;i++){
        double mid = (l+r)/2.0;
        int cnt=k;
        for(int j=n;j>=1;j--){

            if((mid * d[j].v / h)>=1.0*cnt) cnt--;
        }
        if(cnt<=0) r=mid;
        else l=mid;
    }
    int cnt=k;
    for(int j=n;j>=1;j--){
//        int temp=(int)(r*d[j].v/h);
        if((r * d[j].v / h)>=1.0*cnt) ans[cnt--]=d[j].pos;
        if(cnt==0) break;
    }
    for(int i=1;i<=k;i++) cout<<ans[i]<<" ";
    return 0;
}