蹭兄弟学校的题目做还不用自己出题的感觉是真的爽
题目描述
nodgd有一架快要坏掉的天平,这架天平右边的支架有问题,如果右边的总重量比左边多太多,天平就彻底坏掉了。现在nodgd手上有n种砝码,质量分别为m0,m1,m2,...,mn-1,每种砝码有k个。现在要把这n×k个砝码逐个放到天平上,每个砝码都可以放到天平的左边或者右边。放砝码的过程中,天平右边的总重量减去左边的总重量,必须严格小于已经放上天平的最重的一个砝码。如果L,R分别表示已经放上天平左边和右边砝码质量的可重集合,则任何时候都要满足
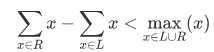
nodgd想知道放砝码的方案总数,答案mod 998,244,353后的值。两种放砝码的方法如果每次放上的砝码质量和放的位置都一样,则认为是相同的。输入格式输入文件。输入一行,包含三个正整数,含义如题目描述中所述。输出格式输出文件输出一个整数,放砝码方案总数后的值。
输入格式
输入一行,包含三个正整数n,m,k,含义如题目描述中所述。
输出格式
输出一个整数,放砝码方案总数mod 998,244,353后的值。
输入样例
2 2 1
输出样例
3
样例说明
质量为1,2的砝码各有1个。如果先放质量为1的砝码,则两个砝码都只能放左边,有1种方案。如果先放质量为2的砝码再放质量为1的砝码,则质量为2的砝码只能放左边,质量为1的砝码随便放,有2种方案。共3种方案。
数据规模与约定
对于30%的数据,n×k<=12;
对于另外20%的数据,m=2,k=1;
对于另外另外20%的数据,m=3,k=2;
对于100%的数据,1≤n×k≤107,k<m≤107。
分析
这道题我们拿到题目的版本要简单一些,是这个亚子的

(你™怎么连人名都换了)
所以我们先来证明一下在这个题目中
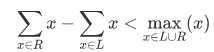
与最重的砝码个数左边应该不小于右边是等价的
对于一个质量为mi砝码,我们可以发现,它的质量其实是 比所有比它质量小的砝码 的质量之和还要大的,
所有比它质量小的砝码 的质量之和可表示为
k×(m0+m1+m2+m3+m4+...+mi-1)=k×$frac {m^i-m^0}{m-1}$
显然这个函数随k单调递增,又因为k<m,即k最大为m-1
所以最大值为
k×$frac {m^i-m^0}{m-1}$ =(m-1)×$frac {m^i-m^0}{m-1}$ =mi-m0<mi
所以天平是否会坏掉只与当前最大砝码的摆放方式有关。
然而这只是这个题目的第一步
接下来我们开始正片

对于这种看一眼就很懵不知道怎么搞的题,我们可以考虑递推
如果固定n,由k推到k+1,增加的砝码质量都不同,不是很好推,所以考虑固定k由n推到n+1
我们试着从有n-1种砝码,每种砝码k个的情况推到n种砝码,每种砝码k个的情况。
设ansi表示i种砝码,每种砝码k个的方案数
不妨假设新增加的k个砝码是质量最小的那一堆(因为不会推最大的那一堆
那么根据样例的提示,对于第一个放上去的砝码进行讨论就有两种情况,一种是第一个放新增加,同时也是质量最小的砝码
另一种是放其它的,也是质量比新加的砝码质量要大的砝码。
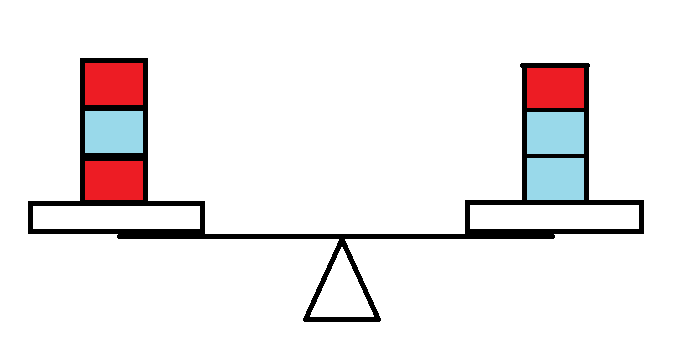
如图,蓝色表示新的,红色表示以前的。
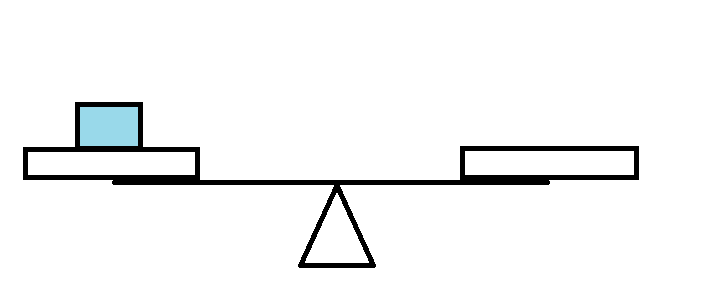
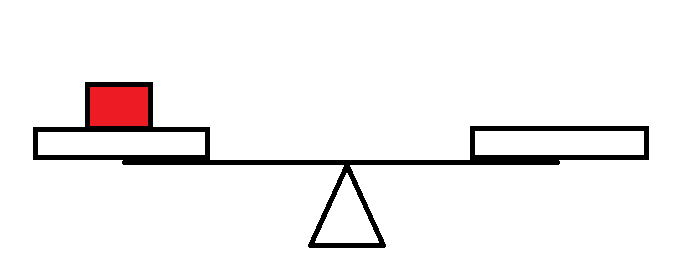
情形一 情形二
对于第二种情况,天平是否会坏掉从一开始就与我们新增加的砝码无关,因为它们质量最小,
而天平是否会坏掉只与当前最大砝码的摆放方式有关。
所以这些砝码是可以乱放的,可以看作是插入到之前的砝码之中,但不能放到开头,而且每种砝码有左右两种选择
第二种情况的方案数就是ansn-1*C(nk-1,k)*2k
再回头来看看第一种情况,反正我还是觉得没什么思路
不过我们可以把第二种情形扩展一下,让它普遍一些。
第二种情况相当于在放第1个砝码的时候就放了质量比新增加的砝码大的砝码
而第一种情况相当于在放第i+1个砝码的时候就放了质量比新增加的砝码大的砝码(1≤i≤k)
两种情况合起来就是在放第i+1个砝码的时候就放了质量比新增加的砝码大的砝码(0≤i≤k)
那么就剩下k-i个砝码可以在以后乱放。
而前i个砝码的放置一定是合法的。
我们设f(i)表示i个同种砝码放置合法的方案数
那么总的方案数就是
ansn=ansn-1$sum_{i=0}^k f(i) C_{nk-i-1}^{k-i}2^{k-i}$
只要知道f(i)就可以知道递推式了
而且ans1=f(k)
所以只要知道f(i)就可以计算答案
接下来我们来推一下f(i)
既然f(i)表示i个同种砝码放置合法的方案数
合法的意思就是左边的砝码不少于右边砝码
感觉有点像卡特兰数
我们可以用几何法解决

如果假设放左边一个砝码相当于向右走一步,放右边一个砝码相当于向上走一步
那么f(i)就表示从(0,0)走到直线x+y=i(y>=0)且不能越过直线x=y的方案数
越过x=y的情况时肯定到达了y=x+1(绿色直线)
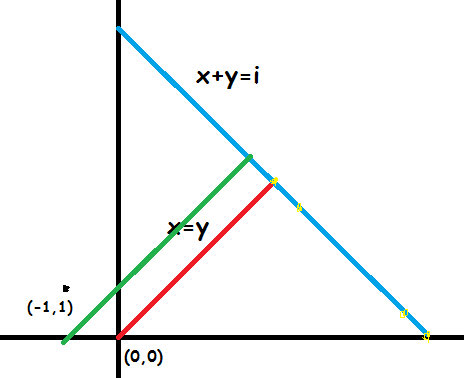
作(0,0)关于y=x+1的对称点(-1,1),那么f(i)就是(0,0)走到黄色点的方案数-(-1,1)走到黄色点的方案数(有些黄色点没画)
所以
f(i)=C(i,i/2)-C(i,i/2+1)+C(i,i/2+1)-C(i,i/2+2).....+C(i,0)-C(i,-1)
=C(i,i/2)-C(i,-1)
=C(i,i/2)
我们终于可以得出答案
ans1=C_{k}^{k/2}
ansn=ansn-1$sum_{i=0}^k f(i) C_{nk-i-1}^{k-i}2^{k-i}$
时间复杂度为O(nk)
分析过程贼长但最后依然还是挺短的代码
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=20000005;
const int mod=998244353;
int n,m,k,ans,fac[maxn],inv[maxn],bw[maxn],f[maxn];
int qp(int a,int k)
{
int res=1;
while(k){if(k&1)res=1ll*res*a%mod;a=1ll*a*a%mod;k>>=1;}
return res;
}
void prework()
{
bw[0]=fac[0]=1;
for(int i=1;i<=20000000;i++)bw[i]=2ll*bw[i-1]%mod,fac[i]=1ll*i*fac[i-1]%mod;
inv[20000000]=qp(fac[20000000],mod-2);
for(int i=19999999;i>=0;i--)inv[i]=1ll*(i+1)*inv[i+1]%mod;
}
int C(int a,int b){return 1ll*fac[a]*inv[a-b]%mod*inv[b]%mod;}
int main()
{
scanf("%d%d%d",&n,&m,&k);
prework();ans=C(k,k/2);
for(int i=2;i<=n;i++)
{
int t=0;
for(int j=0;j<=k;j++)
t=(t+1ll*C(j,j/2)*bw[k-j]%mod*C(i*k-j-1,k-j)%mod)%mod;
ans=1ll*ans*t%mod;
}
printf("%d
",ans);
}