【洛谷】P4594 [COCI2011-2012#5] BLOKOVI

  本来已经有一个专门记录洛谷题目的博客了，但这个题之毒瘤。。。。。。

  为你专门写一篇总行了吧。。。。。。

  传送门

  先说一句，这个题每次摆放都靠到最右边不一定是最优的

  因为它可以这个亚子

 

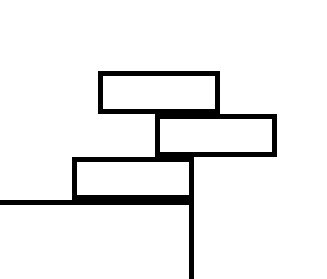
  就是说上面那个块太重了，可以把下面向右伸的块压住（这不就是样例吗嘚瑟个啥

  接下来说一说正解的思路

  从下往上放的时候，每一次加入都要考虑每一层重心的变化，很麻烦，所以还是从上往下放（相当于插入

  然后发现插入最底下那一层的矩形时，因为这个矩形不能变，所以上方的n-1个矩形肯定是越靠右越优

  最右的时候就是当上方的n-1矩形的重心恰好在它的右端点。

  此时答案就相当于最右端点到重心的距离

  所以我们可以去求最右端点到当前重心距离的最值

  设$dp[i]$表示前$i$个矩形摆放好后最右端点到它们的重心距离的最大值

  接下来可以来试着从$dp[i-1]$递推到$dp[i]$

 

  先从理论计算的角度来看，接下来的转移方法来自别人的博客，思路是枚举前$i-1$个矩形的重心在第$i$个矩形的位置然后找到最值。

  我们假设已知当前积木$i$质量$mass$,之前所有积木质量$M$,
  以积木$i$的左端点为原点，设$i−1$块积木构成的整体的重心在$X$轴的坐标为$x,x∈[0,2]$
  新的重心横坐标
  $$NewCentre=frac {M imes x+1 imes mass} {M+mass} =frac {M imes x+mass}{M+mass}$$
  新的最右端可能有两个，一个是之前的那个最右端，另一个是当前木块的右端,取$max$得到坐标就好了
  $$Right=Max(2,x+dp[i−1])$$
  所以
  $$dp[i]=Max(2,x+dp[i−1])− frac {M imes x+mass}{M+mass}$$
  $$=frac {Max(2 imes M+2 imes mass,x imes (M+mass)+dp[i−1] imes(M+mass))−M imes x−mass}{M+mass}$$
  $$=frac {Max((2−x) imes M+mass,(x−1) imes mass+dp[i−1] imes (M+mass))}{M+mass}$$
  可以发现，$Max()$中的两个式子，一个是随着$x$上升单调递增，一个是随着$x$上升单调递减的，均满足单调性，因此直接考虑x=0,2完全是可以的，换句话说，即一个是重心在左端点，一个是重心在右端点.所以答案是在这两个地方产生的。

  所以转移的时候直接枚举前$i-1$个矩形的重心是放在左端点还是右端点就行了。

  也可以画图理解

 

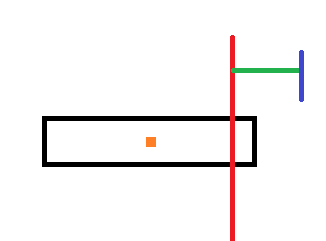
  红线代表前i-1个矩形的重心所在的垂直于地面的直线，深蓝色是最右端的位置，绿色就是$dp[i-1]$，橙色是第$i$个矩形的重心

  先明确目标，我们要找到新重心到原来的右端点距离，即新重心到蓝色直线的距离的最值，

  还有新重心到当前矩形的右端点的距离的最值

  先求最右端点到新重心距离的最值，我们把新的重心所在直线画出来

 

  就是这条浅紫色的线

  根据物理的杠杆原理（雾，其实是感性理解）

  新重心所在直线到前i-1个矩形重心所在直线的距离 与 新重心所在直线到第i个矩形重心所在直线的距离 的比例为它们重量的反比

  

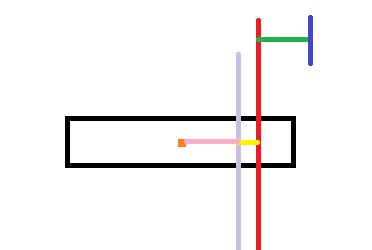
  即黄色线段与粉色线段长度的比例为重量的反比。

  这个比例我们不用知道具体是多少，只需要知道这个比例只跟重量有关，而前i-1个矩形的重量与第i个矩形的重量是固定的

  所以黄色线段与粉色线段的比例是固定的

  又发现黄色线段加上粉色线段就是橙色点到红色线段的距离，即原来的两个重心所在直线的距离

  所以，原来的两个重心所在直线的距离越长，黄色线段越长。

  而新重心到原来右端点的距离就是黄色线段加上绿色线段，且绿色线段的长度是固定的

  所以，原来的两个重心所在直线的距离越长，新重心到以前右端点的距离越长。

  当然，这只限于红线在右边的情况，还有红线在左边的情况

  

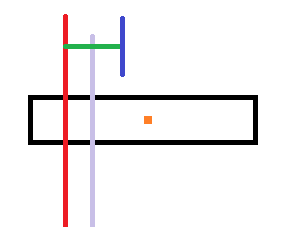
  总之最后可以得出结论，红线越往右，新重心到以前右端点的距离越长，最右的时候就是红线恰好在矩形的右端点处。

  接下来看新重心到矩形右端点的最值

  就是浅紫色直线到矩形右端点的最值

  显然，前i-1的矩形的重心越靠左，新的重心越靠左

  即红色直线越靠左，浅色直线越靠左，距离矩形右端点的距离就越远

  红色直线最左在矩形左端点，此时新重心到矩形右端点的距离取到最值

  所以

  新重心到矩形右端点的最值是当红色直线在矩形左端点取得

  新重心到以前右端点的最值是当红色直线在矩形右端点取得

  所以只需要考虑原来重心在左端点和原来重心在右端点的情况

  最终思路就是把矩形从上往下放，记录重心道最右端点的距离，

  每次转移只考虑之前重心在左端点和之前重心在右端点的情况

  Code

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=300005;
int n,a[maxn];double sum,ans;
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)scanf("%d",&a[i]);
    for(int i=n;i>1;i--)
    {
        sum+=a[i];
        double del=double(a[i])/sum;
        ans=max(ans,max(ans+del,2-del));
    }
    printf("%.8lf",ans);
}