蒜厂年会|计蒜客2019蓝桥杯省赛 B 组模拟赛（一）

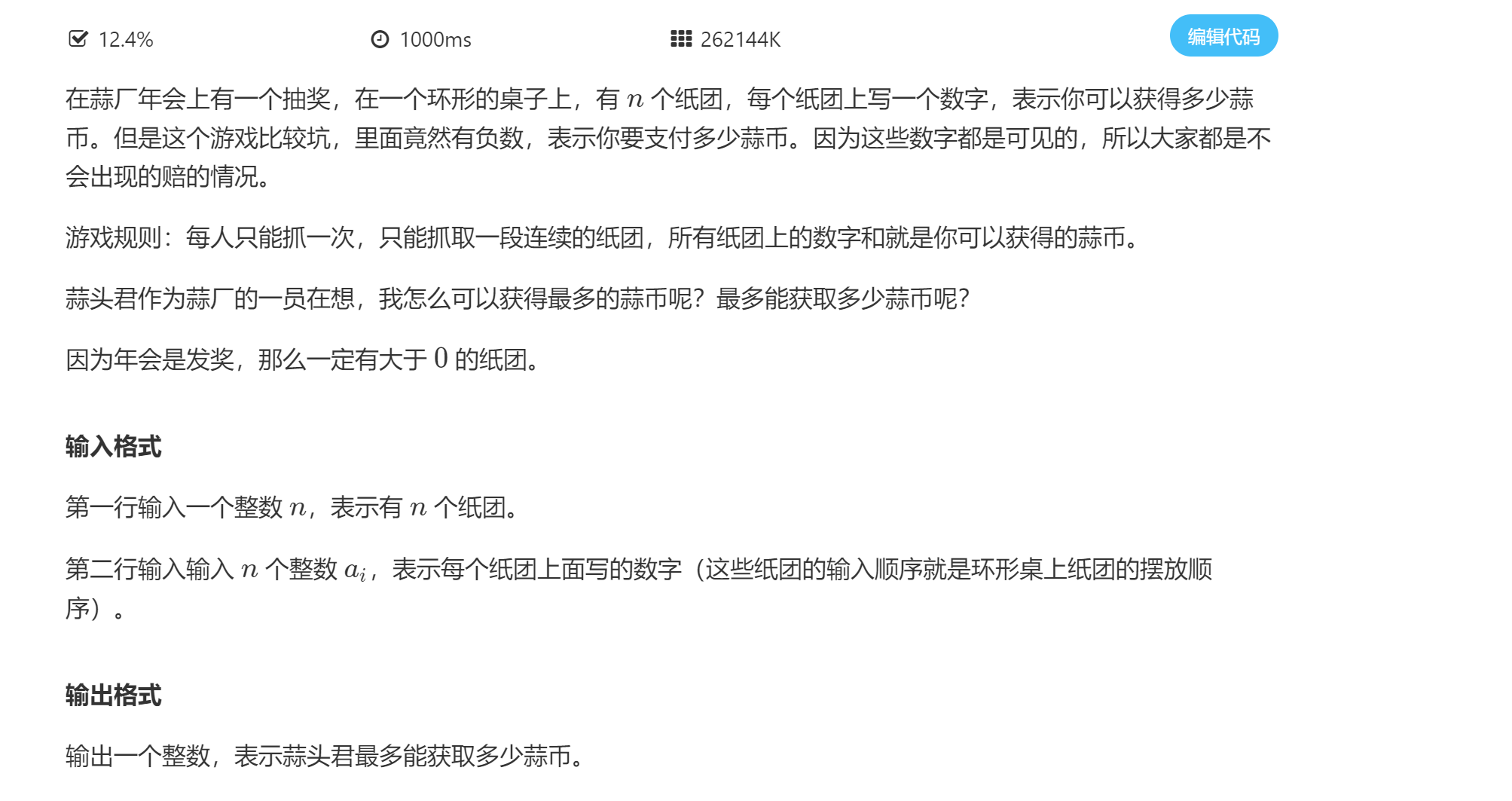
思路一：环形数组拆分成普通数组（通过搬运复制数据到尾部），再求前缀和，找出最大前缀和。因为枚举了每一个起点 所以最大连续和也一定出现在前缀和中！

思路二：1、如果子序列的最大和在 1 到 n 的范围内，直接输出最大和即可 2、如果子序列的最大和横跨了尾部和头部，则先求出连续的最小子序列和然后用总和减去最小子串和就是最大子串和 所以求 1 到 n 中的最大和最小的连续子序列和（记为Mx，和Mi），然后输出 Mx 和 sum-Mi 中的最大值即可。

思路三： 求最大连续子序列的题目(dp)，只是变成了环。变成了环，那就用点贪心策略，从最小的那段连续数(有点像把那段最小的舍去的韵味，其实并没有)后面开始dp。

比如：1 -2 -2 1 -1 4 从1 -2 -2 1 -1 4      从下划线的地方开始dp

          1 -2 -2 15 -3 4  从1 -2 -2 15 -3 4      从下划线的地方开始dp

代码一：60%。暴力，枚举数组的起点，环形数组通过把0~起点这段数据搬运到尾部，形成新的数组。再对新数组球前缀和，找出最大的前缀和即可。

#include<iostream>
using namespace std;

int n;
long long arr[20010];
long long s[20010];

int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>arr[i];
	}
	int maxtt = -1;
	int i;
	for(i = 1;i<=n;i++){
		//搬运数据
		for(int j=1;j<i;j++){ 
			arr[n+j] = arr[j];
		}
		int len = n + i;
		//求出最大的连续和(前缀和)
		s[i-1] = 0;
		for(int p = i;p<=len;p++){
			s[p] = s[p-1] + arr[p];
			if(s[p] > maxtt) maxtt = s[p];
		}
		
	}
	cout<<maxtt<<endl;
	return 0;	
} 

代码二：100%数据

#include <bits/stdc++.h>
# define MAXN 200005
# define INFI 0x3f3f3f3f
 
using namespace std;
long long sum,mx=0,mi=0,Mx=0,Mi=0;
long long num[MAXN],n;
int main()
{
//  freopen("in.txt","r",stdin);
    ios::sync_with_stdio(false);
    cin >> n;
    memset(num,0,sizeof(num));
    Mx = -INFI;
    Mi = INFI;
    mx = mi = sum = 0;
    long long tmp = 0;
    for(int i=0; i<n; ++i)
    {
        cin >> num[i];
        sum += num[i];
        mx += num[i];
        mi += num[i];
        Mx = max(Mx,mx);
        Mi = min(Mi,mi);
        if(mi > 0) mi = 0;
        if(mx < 0) mx = 0;
    }
    cout << max(sum-Mi,Mx) <<endl;
    return 0;
}

代码三:对应思路三，循环数组，找到最小的连续和，从这个连续和后面开始找最大连续和

#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
#define ms(a) memset(a,0,sizeof(a))
using namespace std;

ll a[1000006];

int main()
{
	ll n;
	while(~scanf("%lld",&n))
	{
		ll minn=0,mi=inf,t;
		for(ll i=0;i<n;i++){
			scanf("%lld",&a[i]);
			minn+=a[i];//
			if(mi>minn){//记录哪段是最小（包括负的）
				mi=minn;
				t=i;
			}
			if(minn>0)
				minn=0;
		}
		ll ans=0,mk=0;
		ll l=(t+1)%n,r=t;//从那段最小的后面开始dp
		while(l!=r)
		{
			ans+=a[l];
			mk=max(ans,mk);//存最大
			if(ans<0){//负的置零
				ans=0;
			}
			l=(l+1)%n;
		}
		ans+=a[r];//这段是防止全都是正的
		mk=max(ans,mk);
		if(ans<0){
			ans=0;
		}
		cout<<mk<<endl;
	}
	
	return 0;
}