Trie字典树
Trie字典树又称前缀树,顾名思义,是查询前缀匹配的一种树形数据结构
可以分为插入(创建) 和 查询两部分。参考地址极客时间
下图为插入字符串的过程:

创建完成后,每个字符串最后一个字母标记为终结点(图中显示为红色)
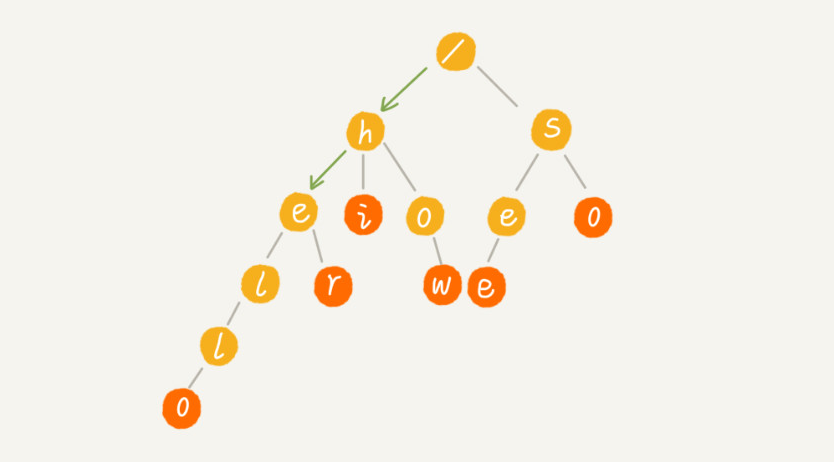
下图为查询字符串:“her”的过程:绿色箭头表示查询路径
我们将要查找的字符串分割成单个的字符 h,e,r,一个一个查询
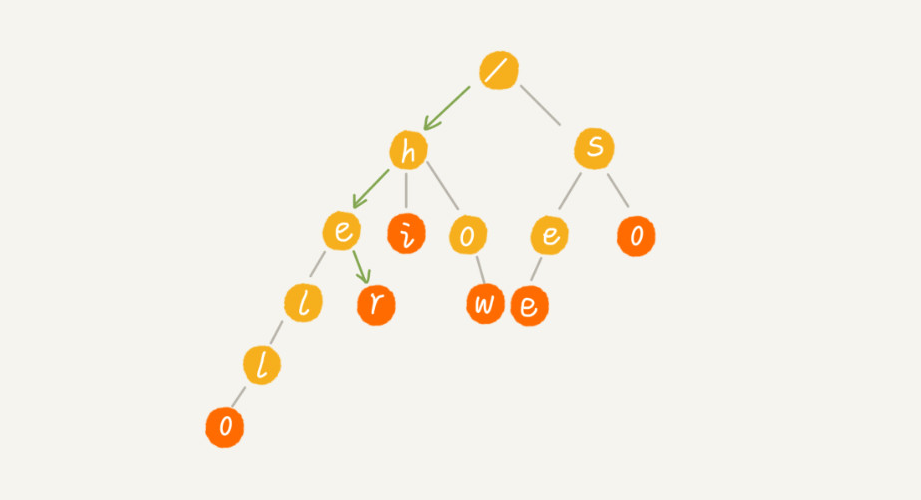
下图为查询字符串:“he”的过程:绿色箭头表示查询路径
因为‘e’不是终结点,所以不能完全匹配上。
Trie字典树的实现
1.首先是字典树 数据结构定义的代码实现
树形结构,类比于二叉树的存储嘛,每个结点两条分支(二叉树);
而字典树,每个节点可以最多有 26个分支(存储英文字母)。
1-1二维数组存储字母
int trie[MAX_NODE][26];//MAX_NODE表示结点数量,每个结点有26个字母结点
int k;
MAX_NODE表示结点数量,每个结点有26个字母结点
Trie[i][j]的值是0,表示trie树中i号节点,并没有一条连出去的边满足边上的字符标识是字符集中第j个字符(从0开始);
trie[i][j]的值是正整数x表示trie树中i号节点,有一条连出去的边满足边上的字符标识是字符集中第j个字符,并且
这条边的终点是x号节点。
1-2链表
我这里用C++中的vector实现,
vector< pair<char, int> > trie[MAX_NODE];
int k;
也可以写一个真正的链表,包含二元组字段<char,int>型的对应关系
1-3hash,
map<char, int> trie[MAX_NODE];
每次我们想找i号节点有没有标识
是某个字符ch的边时,只要看trie[i][ch]的值即可
但是实际上map时空复杂度的常数都比较大
2.插入 和 查询 两个函数的代码实现
插入 查询 实际上是类似的,就是从树的根开始往下遍历,
2-1插入:从树的根开始往下遍历,到达一个结点,没有这个字母就插入到这个结点下,作为这个结点的子节点
基于二维数组结构的插入功能实现
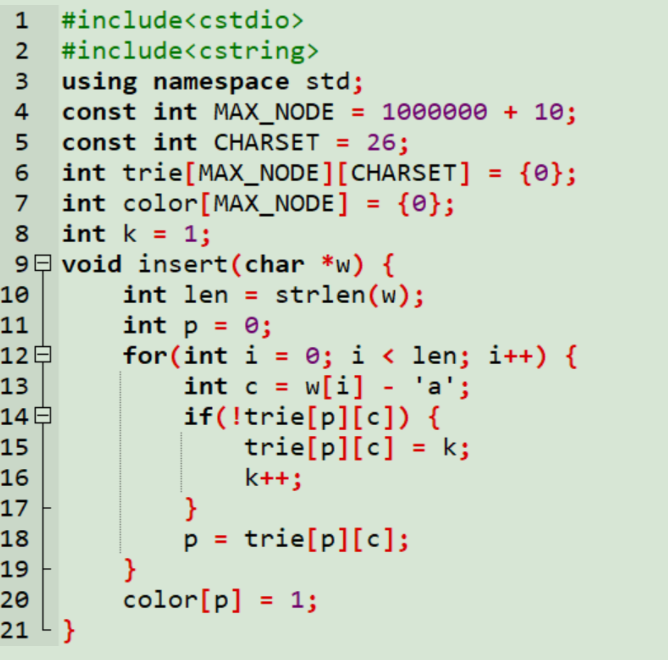
代码的第6~8行,一开始trie[][]被初始化为0,保证每个节点被创建出来时,都没有子节点。K初
始化为1表示一开始只有1个节点,也就是0号节点根节点。Color是用来标记一个节点是不是终结
点。Color[i]=1标识i号节点是终结点。
第9~21行是插入函数insert(w),w是字符指针,实际上可以看作是一个字符串。
第11行是p从0号节点开始。
第12~19行是依次插入w的每一个字符。
第13行是计算w[i]是字符集第几个字符,这里我们假设字符集只包含26个小写字母。
第14~17行是如果p没有连出标识是w[i]的边,那么就创建一个。这里新创建的节点一定就是k号节
点。所谓创建新节点实际上也没什么可创建的,新节点就是个编号。所以我们直接令trie[i][c]=k
即可,然后将k累加1,整个创建过程就完成了。
第18行是沿着标记着w[i]的边移动到下一个节点。
最后第20行,是将最后到达的节点p标记为终结点。
2-2查询:从树的根开始往下遍历,查看是否匹配上当前正在查的单词
基于二维数组结构的查询功能实现

第24行是从p=0也就是根节点开始。
第25~29行是枚举s的每一个字符。
第26行是计算当前字符s[i]在字符集的序号。
第27行是判断p节点有没有连出标识s[i]字符的边,如果没有,说明现在无路可走,直接返回0;如
果有的话,
第28行就是移动到下一个节点。如果整个循环结束还没有return 0,那就说明成功沿着s的每一个
字符到达了p节点。这时只要判断p节点是不是终结点即可,也就是第30行的代
3.完整代码C++版
public class Trie {
private TrieNode root = new TrieNode('/'); // 存储无意义字符
// 往 Trie 树中插入一个字符串
public void insert(char[] text) {
TrieNode p = root;
for (int i = 0; i < text.length; ++i) {
int index = text[i] - 'a';
if (p.children[index] == null) {
TrieNode newNode = new TrieNode(text[i]);
p.children[index] = newNode;
}
p = p.children[index];
}
p.isEndingChar = true;
}
// 在 Trie 树中查找一个字符串
public boolean find(char[] pattern) {
TrieNode p = root;
for (int i = 0; i < pattern.length; ++i) {
int index = pattern[i] - 'a';
if (p.children[index] == null) {
return false; // 不存在 pattern
}
p = p.children[index];
}
if (p.isEndingChar == false) return false; // 不能完全匹配,只是前缀
else return true; // 找到 pattern
}
public class TrieNode {
public char data;
public TrieNode[] children = new TrieNode[26];
public boolean isEndingChar = false;
public TrieNode(char data) {
this.data = data;
}
}
}
Trie字典树的时间复杂度 与 缺点
插入的时间复杂度:O(N),N为所有待插入字符串的长度之和
查询的时间复杂度:O(K),K为待查询字符串的长度
占内存:如果用二维数组实现,每个节点就会额外需要 26*8=208 个字节
优化思路:将每个节点中的数组换成其他数据结构,比如有序数组(可以二分查找)、跳表、散列表、红黑树等。
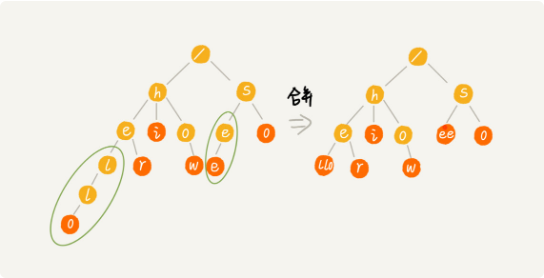
Trie变体,缩点优化:对只有一个子节点的节点,而且此节点不是一个串的结束节点,可以将此节点与子节点合并
Trie字典树的实际应用
1.搜索引擎输入框关键词提示
因为字典树是查找 “与前缀匹配的字符串”,又称为前缀树。
关键词提示就是 查寻找前缀匹配的前缀合适关键词,当然还有更复杂的关键词排名问题,这里不再展开。
2.自动补全功能,如:IDE编译器自动补全,输入法自动补全等
原理与搜索引擎类似。
3.敏感词过滤系统
4.其它
Trie在面试与算法竞赛中的例题
1.hihoCoder1014
解题思路:Trie字典树
首先我们把集合中的N个字符串都插入到trie中。
对于每一个查询s我们在trie中查找s,如果查找过程中无路可走,那么一定没有以s为前缀的字符串。
如果最后停在一个节点p,那我们就要看看以p为根的子树里一共有多少终结点。
终结点的数目就是答案。
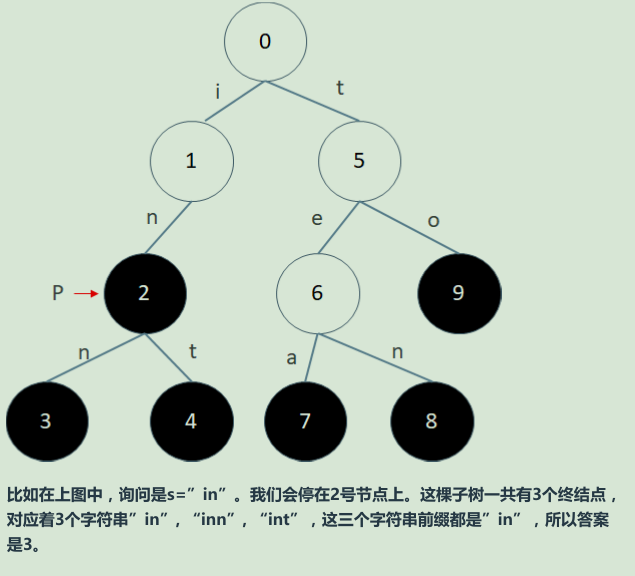
但是如果我们每次都遍历以P为根的子树,那时间复杂度就太高了。解决的办法是用空间换时间,我们增加一个数组intcnt[MAX_NODE]
cnt[i]记录的是以i号节点为根的子树中,有几个终结点。
然后我们每次insert一个字符串的时候,顺便就把沿途的节点的cnt值都+1。
这样就不用每次遍历以P为根的子树,而是直接输出cnt[P]即可。
代码:

2.hihoCoder1107微软面试题
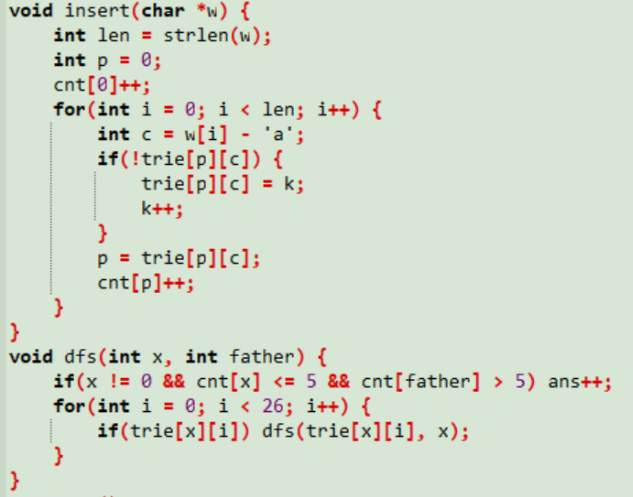
其实就是找一个节点p,满足以p为根的子树中的终结点不多于5个,同时以p的父节点为根的子树中的终结点大于5个。
和上题一样用cnt数组标记,之后dfs查找终结点的数目
3.Trie应用在整数xor异或值最大的题目
给定一个包含N个整数的集合S={A1, A2, A3, … AN}。然
后有M个询问,每次询问给定一个整数X,让你找一个Ai使得Ai xor X的值最大。
首先我们知道一个整数可以用二进制表示成一个01串。比如3=(011)2, 5=(101)2, 4=(100)2……。
我们假设输入的整数都在0~2^32-1之间,于是我们可以用一个长度是32位的01串表示一个整数。
然后对于给定的N个整数A1, A2, A3, … AN,我们把它们对应的01串都插入到一个trie中。注意这里字符集只有0和1,所以整个trie是一棵二叉树。
下面我们举一个例子,为了描述方便,我们假设整数都在0~7之间,也就是可以用3位01串表示。
现在假设S={1, 2, 7},也就是说我们要在Trie中插入{001, 010, 111}:
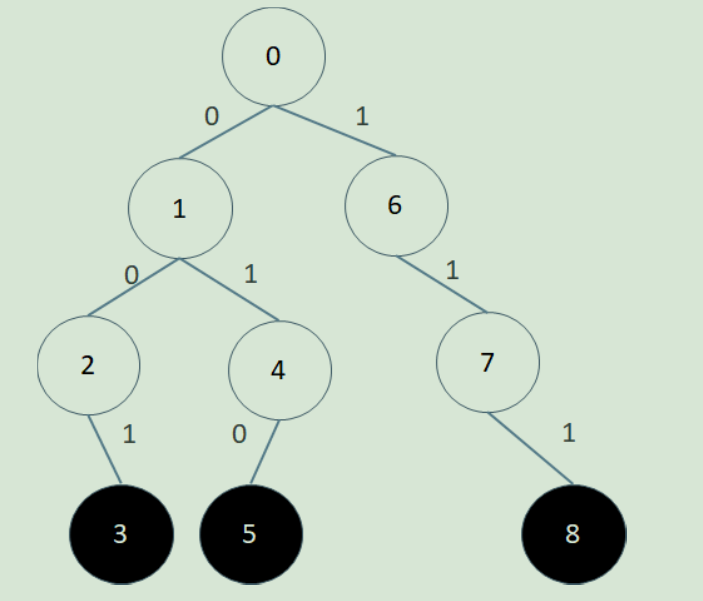
这时假设我们要查询x=4,也就是哪个数和4异或结果最大?4=(100)2,
我们的做法是在trie树中,尽量与4的二进制位反着走。
比如4的第一位(最高位)是1,我们从0出发第一步就尽量沿着0走。因为我们要异或和最大,01相反才能异或值是1。
并且这一步是可以贪心的,也就是说如果有相反的边,那么我们一定沿着这条边走。因为最高位异或得1的话,即便后面都是0, 10000…000也要比最高位是0,后面都是1的011111…111大。
所以我们第一步沿着标识是0的边,移动到了1号节点;4第二位是0,所以我们沿着标识是1的边移动到4号节点;
4的第三位是0,但是4号节点没有标识是1的边,所以我们也只好沿着标识是0的边移动到5号节点。
已经到了终结点,所以5号节点对应的A2=(010)2=2就是我们要求的答案,A2 xor 4 = 6是最大的。