LeetCode 双指针、滑动窗口、单调队列专题

167. 两数之和 II - 输入有序数组

暴力做法O(n^2)：枚举两个数的组合，两层循环

优化，因为具有单调性

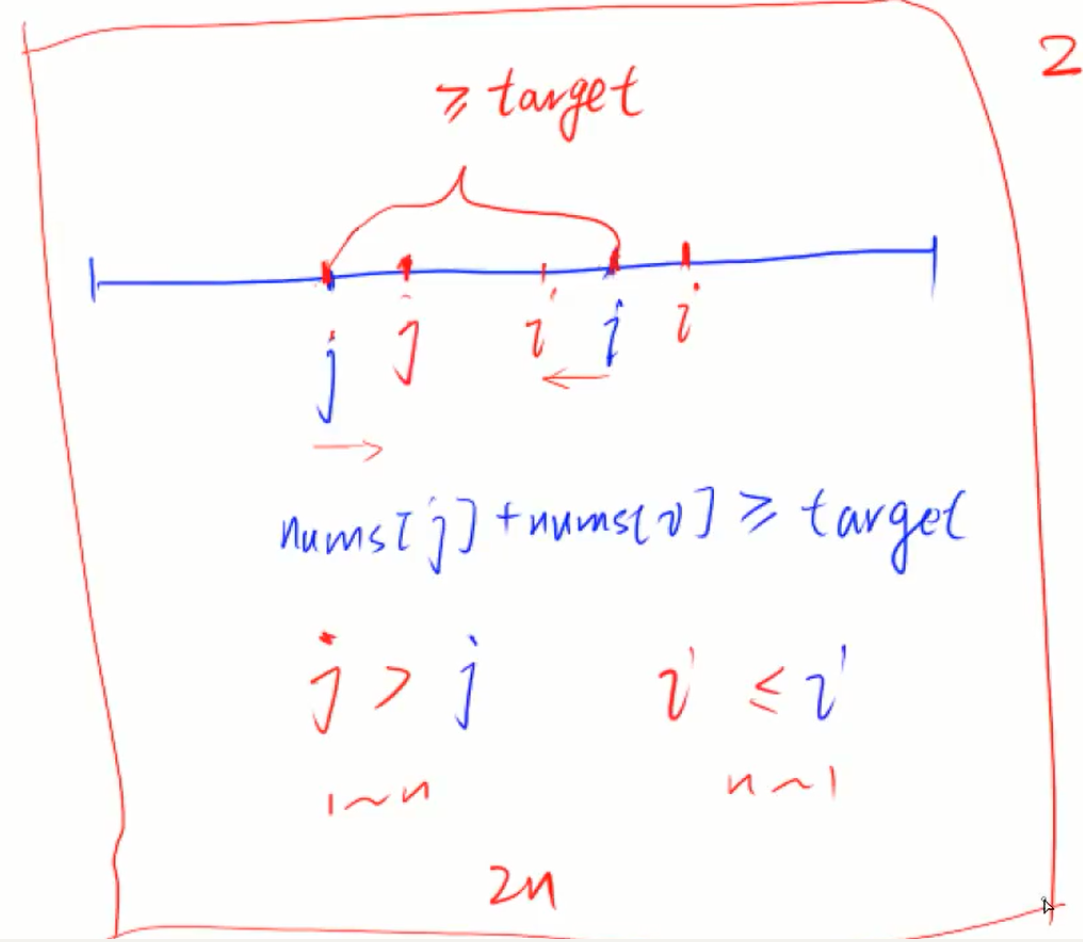
使i和j分别指向数组末尾和开头

对于固定了的a[j]，我们去可以找到一个a[i] 使得 a[j] + a[i] >= target;

然后向右移动j，那么i肯定要向左移动，这就是双指针适用于单调性问题

把两层循环优化到一层循环，复杂度(O(2n))

class Solution {
public:
    vector<int> twoSum(vector<int>& numbers, int target) {
        int n = numbers.size();
        //i向右移动number[i]增大
        //为使得和等于target 必须要将j向左移动 即numbers[j]减小
        for(int i=0,j = n-1;i<n,j>i;i++){
            while(j > i && 
            	numbers[j] + numbers[i] > target) j--;
            if(j > i && numbers[j] + numbers[i] == target) 
            	return 	{i+1,j+1};
        }
        return {-1,-1};
    }
};

方法二：

也能用二分，由于数组中可能有重复元素，所以要判断一下i==j的情况

如下样例：

class Solution {
public:
    vector<int> twoSum(vector<int>& numbers, int target) {
        int n = numbers.size();
        for(int i=0;i<n;i++){ // i + j >= 9  j >= 9-i
            if(numbers[i] > target) break;
            int j= lower_bound(numbers.begin(),numbers.end(),target-numbers[i]) - numbers.begin();
            if(i == j) j = j + 1;
            if(j < n && numbers[i] + numbers[j] == target) return {i+1,j+1};
        }
        return {-1,-1};
    }
};

88. 合并两个有序数组

归并排序的思想，把两个有序序列合并为一个有序序列

看出是双指针，初始时两个指针同时先指向末尾，第三个指针指向下一个存放位置

红指针、蓝指针分别指向自己数组中的最大值，取二者指向的最大值

把两个数组中的比较大的值先放到新答案数组中，然后移动这个指针

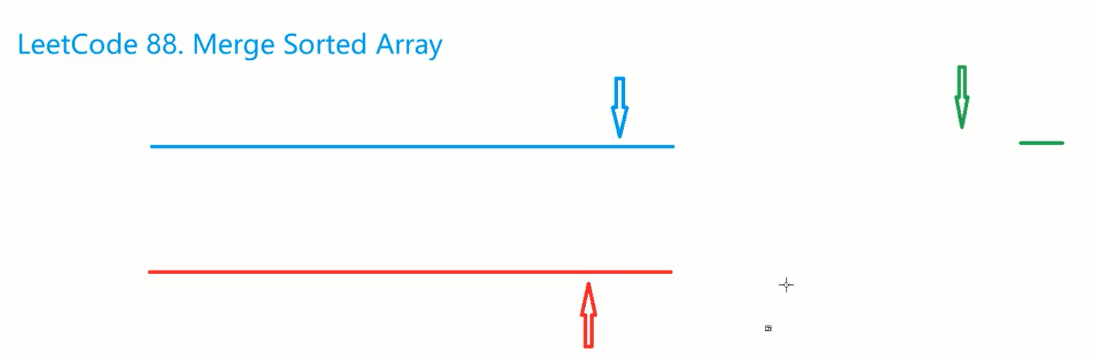
为什么要从大到小来做，因为题目要去存入到第一个数组中
如果从前开始绿色指针会覆盖蓝色数组没用过的数字，而第一个数组末尾的数是空位置，所以可以从大到小来做

注意边界，数组可能为空！

class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
        int p = m-1, q = n-1, r = m + n - 1;
        //注意p和q边界控制
        for(r = m + n - 1; r>=0, p>=0 && q>=0; r--){
            if(nums1[p] >= nums2[q]){
                nums1[r] = nums1[p--];
            }else{
                nums1[r] = nums2[q--];
            }
        }
        while(q >= 0 ) nums1[r--] = nums2[q--];
    }
};

26. 删除排序数组中的重复项

就是unique去重函数

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        return unique(nums.begin(),nums.end()) - nums.begin();
    }
};

两个指针，一个指针指向下一个存放位置
另一个提前判断是否与第一个指针前一个所指向的位置的值相同。

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        int n = nums.size();
        if(n == 0) return 0;
        if(n == 1) return 1;
        int p = 0,q = 1;
        while(p < n && q < n){
            while(q < n && nums[q] == nums[p]) q++;
            if(q < n && nums[q] != nums[p]) nums[++p] = nums[q];
        }
        return p+1;
    }
};

for循环写法，需要注意p不一定在每一次for循环结束就增加，比如最后一次不能满足的时候不增加，把p++写在该增加的地方就可以了

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        int n = nums.size();
        if(n == 0) return 0;
        if(n == 1) return 1;
        int p,q;
        //用for循环不太好控制最终p的值 for循环后p不一定增加 
        for(p = 0,q = 1;q < n && p + 1 < n;){
            while(q < n && nums[q] == nums[p]) q++;
            if(q < n && nums[p] != nums[q]) 
            	nums[++p] = nums[q++];//这个时候p再++
        }
        return p + 1;
    }
};

76. 最小覆盖子串

1.先想暴力写法

枚举所有子串，看这个子层是不是包含全部字母，更新最小符合的子串长度

2.有无单调性，怎么去优化

单调性；假设i~j包含了子串T，那么当i++，j也一定是增加的，这就是单调性

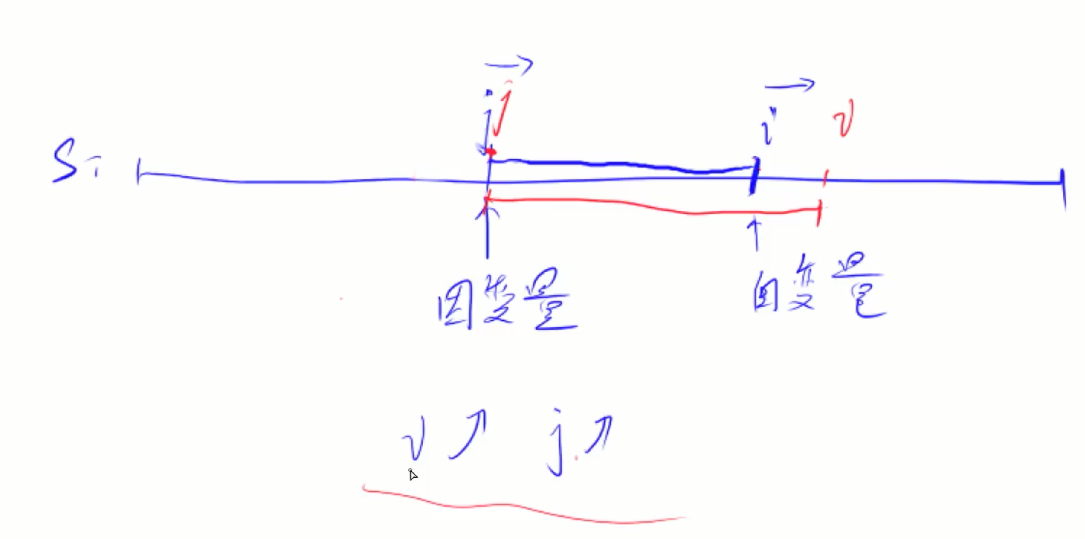
从左往右枚举i，移动j直到满足包含子串T，更新答案；然后自变量i++

i和j都最多走了一遍，i、j不会往后走；所以时间复杂度是 O(2n) 即 O(n)

如何判断i~j的子串包含了串T？
初始时，哈希表统计T里面次数；

另一个哈希表，每次移动j更新当前i~j子串的次数，判断是否满足，两个哈希表比较会超时

超时代码：

class Solution {
public:
    map<char,int> cnt1,cnt2;
    bool check(string &s,string &t){
        for(int i=0;i<t.length();i++){
            if(cnt1[t[i]] < cnt2[t[i]]) return false;
        }
        return true;
    }

    string minWindow(string s, string t) {
        string ans = "";
        int len = 0x3f3f3f3f; 
        int n = s.length();
        int m = t.length();
        if(m > n) return ans;
        if(m == n && s == t) return t;
        for(int i=0;i<m;i++) {
            cnt2[t[i]]++;
        }
        for(int i=0,j = 0;i<n;i++){
            while(j < n && !check(s,t)){
                cnt1[s[j]]++;
                j++;
            }
            if(j < n && check(s,t) && j-i < len){
                ans = s.substr(i,j-i);
                len = j - i;
            }
            if(j == n && check(s,t) && j-i < len){
                ans = s.substr(i,j-i);
                len = j - i;
            }
            cnt1[s[i]]--;
        }
        return ans;
    }
};

优化成只用一个hash表

先统计T里面的次数增加need值；记录需要T中字符的类型和数量

有足够T字符类型和数量后，后面移动左指针来减少need值，更新最小长度，

直到不满足所有类型数量了退出循环

参考题解

class Solution {
public:
    string minWindow(string s, string t) {
        if(s == t) return t;
        unordered_map<char,int> need;
        unordered_map<char,int> have;
        int n = s.length();
        int m = t.length();
        if(m > n) return "";
        int typeNum = 0;
        //统计t里 出现的字符 以及 出现的个数
        for(int i=0;i<m;i++){
            if(need[t[i]] == 0) {
                typeNum++;
                have[t[i]] = 1;
            }
            need[t[i]]++;
        }
        int minLen = n+1;
        int start = 0;
        bool flag = false;
        for(int right = 0,left = 0; right < n; right++){
            char c = s[right];
            if(have[c]) need[c]--;
            if(have[c] && need[c] == 0) typeNum--;
            //当typeNum==0 说明满足了子串包含的条件 
            //这个时候可以考虑逐渐右移动left左指针 更新最小满足长度
            while(typeNum == 0){
                //更新
                if(right - left + 1 < minLen){
                    start = left;
                    minLen = right - left + 1;
                    flag = true;
                }
                //移除left后的变化
                //如果这个字符是t里面的字符就去更新变化
                if(have[s[left]]){
                    //这个left要丢弃了 下次需要的个数就要+1
                    need[s[left]]++; 
                    //如果need字符的个数大于0了 
                    //说明字符typeNum不是全都满足
                    if(need[s[left]] > 0) typeNum++;
                }
                left++;
            }
        }
        if(!flag) return "";
        return s.substr(start,minLen);
    }
};

另一种思路：

string minWindow(string s, string t) {
	unordered_map<char,int> need;
	for(auto c : t) need[c]++;
	int cnt = need.size();
	string res;
	for(int i=0,j=0,c=0;i<s.size();i++){
		if(need[s[i]] == 1) c++;
		need[s[i]]--;
		while(need[s[j]] < 0) 
			need[s[j++]]++;
		if(c == cnt){
			if(res.empty() || res.size() > i - j + 1) 
				res = s.substr(j,i-j+1);
		}
	}
	return res;
}

32. 最长有效括号

有关括号序列的性质：

1.括号对应的括号一定是对应的，不变的

把左括号看成1，右括号看成-1；

2.一个括号序列合法，等价于所有前缀和均>=0，并且总和 = 0

即 从左到右前缀和小于0时，这段肯定不合法；

只能由总和>=0 变成 = 0；才是合法序列；而由总和<=0变成=0就不是合法的序列

正着判断一遍，还需要反着判断一遍

避免正多负少时的 ((((()) 这种情况下，cnt一直大于0的情况时，cnt没有等于0无法统计合法序列

反着一遍相当于)))(((((( ，这样就能统计负的少，合法序列了

class Solution {
public:
    int work(string s){
        int n = s.length();
        int i = 0, start = 0;
        int cnt = 0;
        int ans = 0;
        while(start < n && i < n){
            if(s[i] == '(') cnt++;
            else cnt--;
            if(cnt == 0){
                ans = max(ans,i - start + 1);
            }
            if(cnt < 0) start = i + 1, cnt = 0;
            i++;
        }
        return ans;
    }
    int longestValidParentheses(string s) {
        int ans = work(s);
        reverse(s.begin(),s.end());
        //(：ASCII=40   )：ASCII = 41 异或一下交换
        for(auto &c :s) c^=1;
        return max(work(s),ans);
    }
};

思路二：开一map记录和当前i位置的前缀相同的最远一次的下标；下标相同且中间没有前缀和小于0的非法情况，就是一个合法答案了

如：((()))

前缀和：123210 下标从1开始 则 第0+1与倒1；倒2与第1+1匹配....

再如：(())))()

前缀和：1210 -1 清零记录0的位置 1 0

双指针写法题解

也可以用动态规划做

239. 滑动窗口最大值

长度k的窗口中的最大值

思路一：O(n)枚举窗口起点，O(k)遍历一遍窗口，计算窗口的最小值；总时间复杂度：O(n×k)超时

思路二：单调队列思想：删除冗余元素

单调队列的思想：

总结起来就是：位于窗口左侧，并且还偏小的数字一定不会成为答案；所以可以把这些数移除

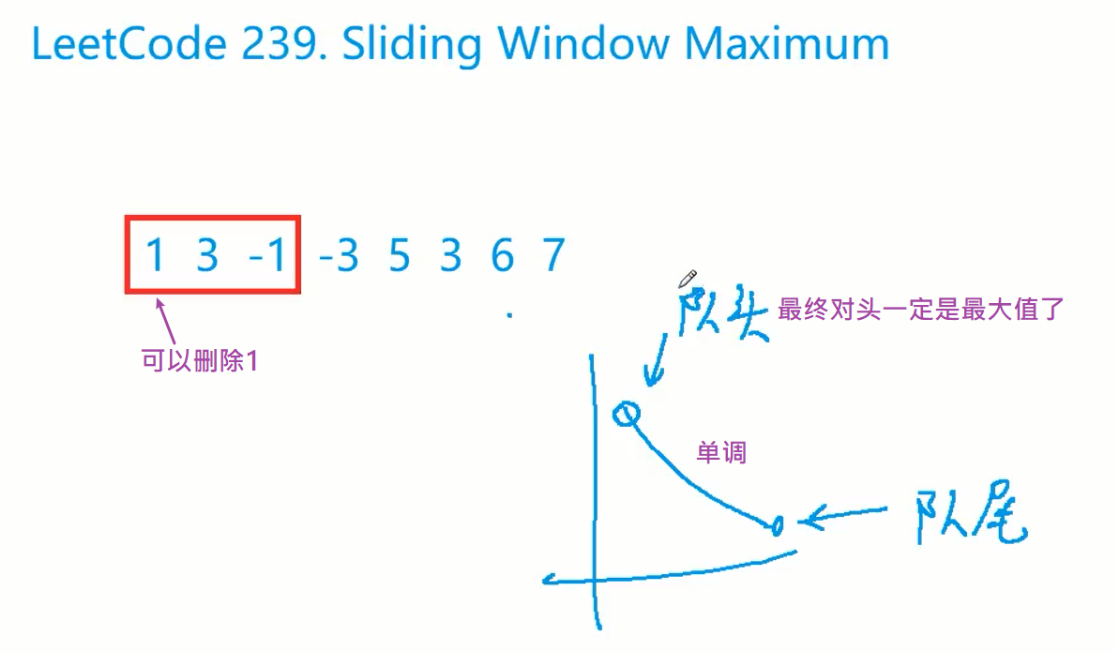
用单调队列，对头删除，队尾添加和删除；用双端队列deque

class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        vector<int> result;
        deque<int> q;
        for(int i=0;i<nums.size();i++){
            //1.先判断队头是否已经在窗口外了 
            //已经在窗口外过期的要出队
            if(q.size() && i - q.front() + 1 > k) 
            	q.pop_front();
            //2.判断队尾是不是冗余 比当前新进来的num[i]值还小就出队
            while(q.size() && 
            	nums[q.back()] < nums[i]) q.pop_back();
            	//3. i入队
            	q.push_back(i); 
            //4. 记录这一轮答案
            if(i >= k - 1) 
            	result.push_back(nums[q.front()]); 
        }
        return result;
    }
};

918. 环形子数组的最大和

拆环成链：环展开成链，两倍长度，限制长度为n

题意就变为，找区间大小长度为1~n的数组连续子段和

固定终点i，找距离1~n的j(窗口左端点，下标比i小)，使得前缀和s[j] - s[i]和最小

问题就转成了"查大小为n的滑动窗口的最小值"问题，查窗口中的最小值s[j]

时间复杂度O(n)

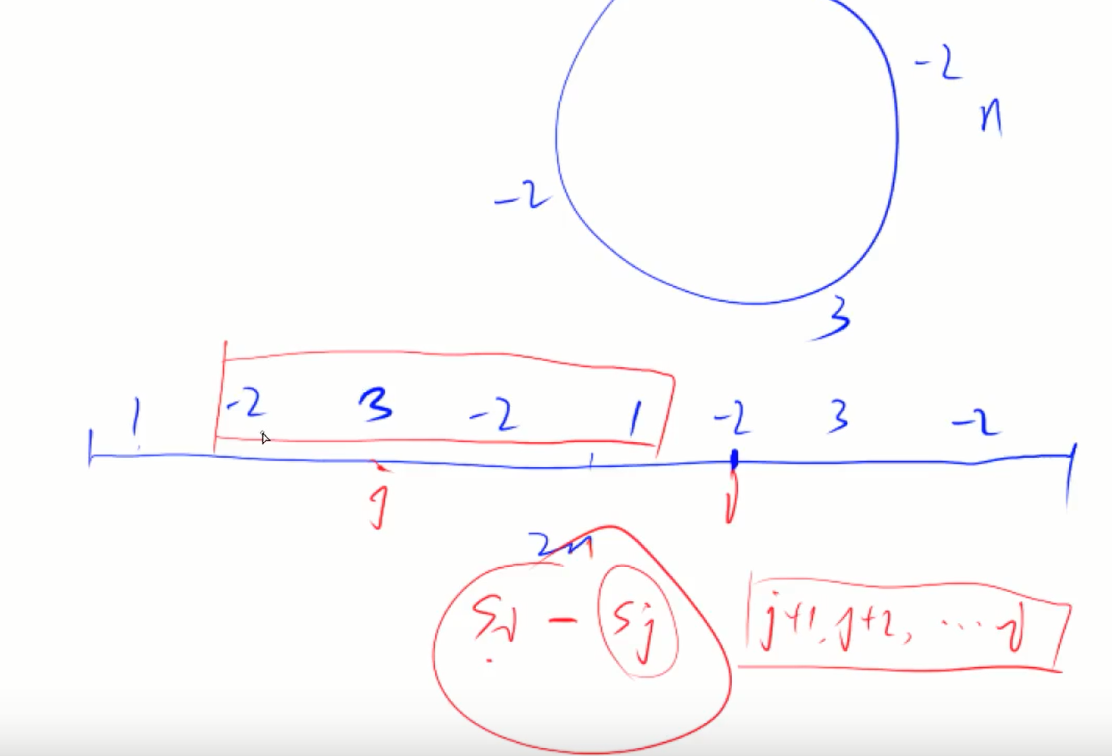
滑动窗口中的值是下标

然后找下标对应的的前缀和最小值j

class Solution {
public:
    int maxSubarraySumCircular(vector<int>& A) {
        int n = A.size();
        for(int i=0;i<n;i++) A.push_back(A[i]);
        deque<int> q;
        vector<int> sum(2*n+1);
        for(int i=1;i<=n*2;i++) sum[i] = sum[i-1] + A[i-1];
        int ans = INT_MIN;
        q.push_back(0);
        for(int i=1;i<=2*n;i++){
            //1.队头是否在窗口
            if(q.size() && i - (q.front()+1) + 1 > n) q.pop_front();
            //2.更新答案 注意要在删除队尾前更新答案
            if(q.size()) ans = max(ans,sum[i] - sum[q.front()]);
            //3.删除队尾冗余
            while(q.size() && sum[q.back()] >= sum[i]) q.pop_back();
            //4.i入队
            q.push_back(i);
        }
        return ans;
    }
};

补充

滑动窗口维护两个边界，可以看成两个指针

可以把滑动窗口看成特殊的双指针算法；

滑动窗口一定是双指针算法，双指针不一定是滑动窗口算法