洛谷 P1231 教辅的组成（网络最大流+拆点加源加汇）

题目背景

滚粗了的HansBug在收拾旧语文书，然而他发现了什么奇妙的东西。

题目描述

蒟蒻HansBug在一本语文书里面发现了一本答案，然而他却明明记得这书应该还包含一份练习题。然而出现在他眼前的书多得数不胜数，其中有书，有答案，有练习册。已知一个完整的书册均应该包含且仅包含一本书、一本练习册和一份答案，然而现在全都乱做了一团。许多书上面的字迹都已经模糊了，然而HansBug还是可以大致判断这是一本书还是练习册或答案，并且能够大致知道一本书和答案以及一本书和练习册的对应关系（即仅仅知道某书和某答案、某书和某练习册有可能相对应，除此以外的均不可能对应）。既然如此，HansBug想知道在这样的情况下，最多可能同时组合成多少个完整的书册。

输入输出格式

输入格式：

第一行包含三个正整数N1、N2、N3，分别表示书的个数、练习册的个数和答案的个数。

第二行包含一个正整数M1，表示书和练习册可能的对应关系个数。

接下来M1行每行包含两个正整数x、y，表示第x本书和第y本练习册可能对应。（1<=x<=N1，1<=y<=N2）

第M1+3行包含一个正整数M2，表述书和答案可能的对应关系个数。

接下来M2行每行包含两个正整数x、y，表示第x本书和第y本答案可能对应。（1<=x<=N1，1<=y<=N3）

输出格式：

输出包含一个正整数，表示最多可能组成完整书册的数目。

输入输出样例

输入样例#1： 

5 3 4
5
4 3
2 2
5 2
5 1
5 3
5
1 3
3 1
2 2
3 3
4 3

输出样例#1： 

2

说明

样例说明：

如题，N1=5，N2=3，N3=4，表示书有5本、练习册有3本、答案有4本。

M1=5，表示书和练习册共有5个可能的对应关系，分别为：书4和练习册3、书2和练习册2、书5和练习册2、书5和练习册1以及书5和练习册3。

M2=5，表示数和答案共有5个可能的对应关系，分别为：书1和答案3、书3和答案1、书2和答案2、书3和答案3以及书4和答案3。

所以，以上情况的话最多可以同时配成两个书册，分别为：书2+练习册2+答案2、书4+练习册3+答案3。

数据规模：

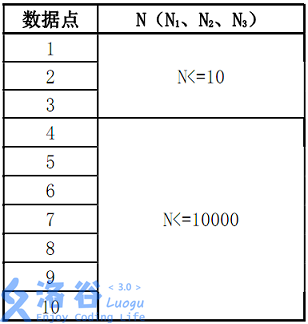
对于数据点1, 2, 3，M1，M2<= 20

对于数据点4~10，M1，M2 <= 20000

Solution：

这道题我调了特别久，主要是看题理解的错误和建图时反向边每有赋容量为0（=_=!），巨尴尬。大家首先容易想到加上超级源S和超级汇T，然后照常建图流量赋1，但是注意该题中一个书可以连多个答案和练习册，这样会出现一种情况，即多个练习本连一本书然后连向多个答案，这样建图显然是错的，即不能把书当作一个节点（因为它具有通过的流量限制，只能流入和流出1的流量，现实意义即一本书只能配对一本答案和练习本），所以我们需要把书拆成两个点之间连一条容量为1的边，然后这两个点分别连向练习册和书本就OK了。还有一个小细节，这里的n1、n2、n3都是从1开始的，直接建边会有冲突（比如n1的1连向n2的1，这样就分不清1是n1还是n2了），这个的处理方法很多，自行解决。

代码：

#include<bits/stdc++.h>
#define il inline
using namespace std;
const int N=100005,inf=2333333;
il int gi()
{
    int a=0;char x=getchar();bool f=0;
    while((x<'0'||x>'9')&&x!='-')x=getchar();
    if(x=='-')x=getchar(),f=1;
    while(x>='0'&&x<='9')a=a*10+x-48,x=getchar();
    return f?-a:a;
}
int s,t,n1,n2,n3,m1,m2,cnt=1,h[N],dis[N],ans;
struct edge{
int to,net,v;
}e[N*2];
il void add(int u,int v,int w)
{
    e[++cnt].to=v,e[cnt].net=h[u],e[cnt].v=w,h[u]=cnt;
    e[++cnt].to=u,e[cnt].net=h[v],e[cnt].v=0,h[v]=cnt;
}
queue<int>q;
il bool bfs()
{
    memset(dis,-1,sizeof(dis));
    dis[s]=0;q.push(s);
    while(!q.empty())
    {
        int u=q.front();q.pop();
        for(int i=h[u];i;i=e[i].net)
        if(dis[e[i].to]==-1&&e[i].v>0)dis[e[i].to]=dis[u]+1,q.push(e[i].to);
    }
    return dis[t]!=-1;
}
il int dfs(int u,int op)
{
    if(u==t)return op;
    int flow=0,used=0;
    for(int i=h[u];i;i=e[i].net)
    {
        int v=e[i].to;
        if(dis[v]==dis[u]+1&&e[i].v>0)
        {
            used=dfs(v,min(op,e[i].v));
            if(!used)continue;
            op-=used;flow+=used;
            e[i].v-=used,e[i^1].v+=used;
            if(!used)break;
        }
    }
    if(!flow)dis[u]=-1;
    return flow;
}
int main()
{
    n1=gi(),n2=gi(),n3=gi(),m1=gi();
    s=0,t=n1*2+n2+n3+5;
    int u,v;
    for(int i=1;i<=m1;i++)
        u=gi(),v=gi(),add(v,u+n2,1);
    m2=gi();
    for(int i=1;i<=m2;i++)
        u=gi(),v=gi(),add(u+n1+n2,v+n1*2+n2,1);
    for(int i=1;i<=n2;i++)add(0,i,1);
    for(int i=1;i<=n3;i++)add(i+n1*2+n2,t,1);
    for(int i=1;i<=n1;i++)add(i+n2,i+n1+n2,1);
    while(bfs())ans+=dfs(s,inf);
    printf("%d
",ans);
    return 0;
}