P2052 [NOI2011]道路修建

题目描述

在 W 星球上有 n 个国家。为了各自国家的经济发展，他们决定在各个国家 之间建设双向道路使得国家之间连通。但是每个国家的国王都很吝啬，他们只愿 意修建恰好 n – 1 条双向道路。 每条道路的修建都要付出一定的费用，这个费用等于道路长度乘以道路两端 的国家个数之差的绝对值。例如，在下图中，虚线所示道路两端分别有 2 个、4 个国家，如果该道路长度为 1，则费用为 1×|2 – 4|=2。图中圆圈里的数字表示国 家的编号。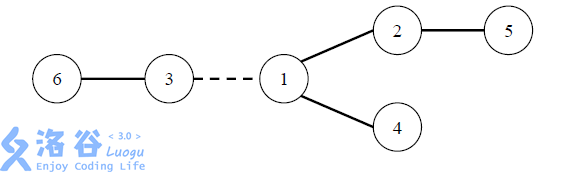

由于国家的数量十分庞大，道路的建造方案有很多种，同时每种方案的修建 费用难以用人工计算，国王们决定找人设计一个软件，对于给定的建造方案，计 算出所需要的费用。请你帮助国王们设计一个这样的软件。

输入输出格式

输入格式：

输入的第一行包含一个整数 n，表示 W 星球上的国家的数量，国家从 1 到 n 编号。 接下来 n – 1 行描述道路建设情况，其中第 i 行包含三个整数 ai、bi和 ci，表 示第 i 条双向道路修建在 ai与 bi两个国家之间，长度为 ci。

输出格式：

输出一个整数，表示修建所有道路所需要的总费用。

输入输出样例

输入样例#1： 

6
1 2 1
1 3 1
1 4 2
6 3 1
5 2 1

输出样例#1： 

20

说明

1≤ai, bi≤n

0≤ci≤10⁶

2≤n≤10⁶

Solution：

　　本题好水啊～

　　我们不妨以$1$为根节点（反正无向连通），$dfs$一遍处理出每个节点子树大小$siz$。

　　然后不难发现，根据题意一条边$e(u-v)$，则花费应该为$|(siz[1]-2*siz[v])|*w(u-v)$（$siz[v]$为该边一边的节点数，$siz[1]-siz[v]$为另一边节点数，相减取绝对值，就是节点数之差），然后累加花费，标记一下该边已经计数。

　　瞎搞一弃就好了。$`～`$

代码：

#include<bits/stdc++.h>
#define il inline
#define ll long long
#define For(i,a,b) for(int (i)=(a);(i)<=(b);(i)++)
using namespace std;
const int N=1e6+7;
int n,to[N<<1],net[N<<1],w[N<<1],h[N<<1],siz[N],cnt;
ll ans;
bool vis[N];

il int gi(){
    int a=0;char x=getchar();bool f=0;
    while((x<'0'||x>'9')&&x!='-')x=getchar();
    if(x=='-')x=getchar(),f=1;
    while(x>='0'&&x<='9')a=(a<<3)+(a<<1)+x-48,x=getchar();
    return f?-a:a;
}

il void add(int u,int v,int c){to[++cnt]=v,net[cnt]=h[u],h[u]=cnt,w[cnt]=c;}

il void prepare(int u,int lst){
    for(int i=h[u];i;i=net[i])
        if(to[i]!=lst)prepare(to[i],u),siz[u]+=siz[to[i]];
}

il void dfs(int x){
    vis[x]=1;
    for(int i=h[x];i;i=net[i])
        if(!vis[to[i]])ans+=abs(siz[1]-2*siz[to[i]])*1ll*w[i],dfs(to[i]);
}

int main(){
    n=gi();
    int x,y,z;
    For(i,1,n)siz[i]=1;
    For(i,1,n-1){
        x=gi(),y=gi(),z=gi();
        add(x,y,z),add(y,x,z);
    }
    prepare(1,1);
    For(i,1,n) if(!vis[i])dfs(i);
    cout<<ans;
    return 0;
}