题目描述
小 C 的兔子不是雪白的,而是五彩缤纷的。每只兔子都有一种颜色,不同的兔子可能有 相同的颜色。小 C 把她标号从 1 到 n 的 n只兔子排成长长的一排,来给他们喂胡萝卜吃。 排列完成后,第 i 只兔子的颜色是 ai。
俗话说得好,“萝卜青菜,各有所爱”。小 C 发现,不同颜色的兔子可能有对胡萝卜的 不同偏好。比如,银色的兔子最喜欢吃金色的胡萝卜,金色的兔子更喜欢吃胡萝卜叶子,而 绿色的兔子却喜欢吃酸一点的胡萝卜……为了满足兔子们的要求,小 C 十分苦恼。所以,为 了使得胡萝卜喂得更加准确,小 C 想知道在区间 [lj,rj]里有多少只颜色为 cj 的兔子。
不过,因为小 C 的兔子们都十分地活跃,它们不是很愿意待在一个固定的位置;与此同 时,小 C 也在根据她知道的信息来给兔子们调整位置。所以,有时编号为 xj和 xj+1 的两 只兔子会交换位置。 小 C 被这一系列麻烦事给难住了。你能帮帮她吗?
输入输出格式
输入格式:
从标准输入中读入数据。 输入第 1 行两个正整数 n , m。
输入第 2 行 n 个正整数,第 i 个数表示第 i只兔子的颜色 ai 。
输入接下来 m 行,每行为以下两种中的一种:
-
“ 1 lj rj cj ” :询问在区间 [lj,rj]里有多少只颜色为 cj的兔子;
-
“ 2 xj ”: xj 和 xj+1 两只兔子交换了位置。
输出格式:
输出到标准输出中。
对于每个 1 操作,输出一行一个正整数,表示你对于这个询问的答案。
输入输出样例
6 5
1 2 3 2 3 3
1 1 3 2
1 4 6 3
2 3
1 1 3 2
1 4 6 3
1
2
2
3
说明
【样例 1 说明】
前两个 1 操作和后两个 1 操作对应相同;在第三次的 2 操作后,3 号兔子和 4 号兔子
交换了位置,序列变为 1 2 2 3 3 3。
【数据范围与约定】
子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难,可以尝试只解 决一部分测试数据。 对于所有测试点,有 1≤lj<rj≤n,1≤xj<n 。 每个测试点的数据规模及特点如下表:
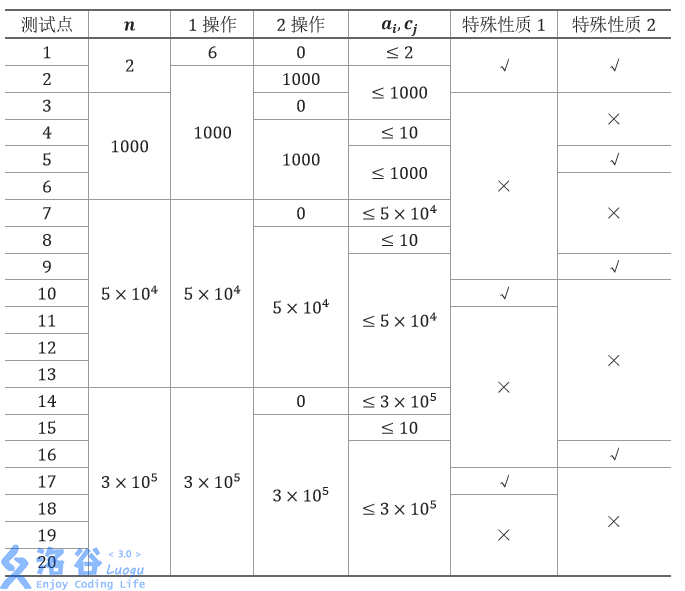
特殊性质 1:保证对于所有操作 1,有 ∣rj−lj∣≤20 或 ∣rj−lj∣≤n−20。
特殊性质 2:保证不会有两只相同颜色的兔子。
Solution:
$6$月初真的不适合我码题,什么错误都出来了,调试总是搞半天`~`。。。
算是主席树模板题,维护每个颜色建立主席树,因为颜色数$leq 3*10^5$,所以不用离散。
那么每次加入一个颜色,就更新一下节点信息,没有节点就新建一下。
修改直接将第$x$和$x+1$位置颜色节点清$0$,然后重新更新一下这两个节点的颜色信息,再交换一下原数组中的颜色。
最后查询时,就一直沿着所需颜色的节点在要求区间范围内往下找,累加求和就好了。
(本题卡常,注意常数优化!)
代码:
#include<bits/stdc++.h> #define il inline #define For(i,a,b) for(int (i)=(a);(i)<=(b);(i)++) using namespace std; const int N=300005; int n,m,sum[N*30],a[N],rt[N],ls[N*30],rs[N*30],cnt; il int gi(){ int a=0;char x=getchar(); while(x<'0'||x>'9')x=getchar(); while(x>='0'&&x<='9')a=(a<<3)+(a<<1)+x-48,x=getchar(); return a; } il void update(int l,int r,int pos,int c,int &rt){ if(!rt)rt=++cnt; sum[rt]+=c; if(l==r)return; int m=l+r>>1; if(pos<=m)update(l,m,pos,c,ls[rt]); else update(m+1,r,pos,c,rs[rt]); } il int query(int L,int R,int l,int r,int rt){ if(!rt)return 0; if(L<=l&&R>=r)return sum[rt]; int m=l+r>>1,ret=0; if(L<=m)ret+=query(L,R,l,m,ls[rt]); if(m<R) ret+=query(L,R,m+1,r,rs[rt]); return ret; } int main(){ n=gi(),m=gi(); For(i,1,n) a[i]=gi(),update(1,n,i,1,rt[a[i]]); int f,x,y,z; while(m--){ f=gi(); if(f==1){ x=gi(),y=gi(),z=gi(); printf("%d ",query(x,y,1,n,rt[z])); } else { x=gi(); update(1,n,x,-1,rt[a[x]]); update(1,n,x+1,-1,rt[a[x+1]]); update(1,n,x+1,1,rt[a[x]]); update(1,n,x,1,rt[a[x+1]]); swap(a[x],a[x+1]); } } return 0; }