算法与数据结构

衡量算法好坏的指标

1.时间复杂度

我们使用程序执行的大概次数来表示时间复杂度，使用O()记

如何一眼判断时间复杂度？

• 循环减半的过程O(logn)

• 几次循环就是n的几次方的复杂度

2.空间复杂度

当前程序运行的时候，是否需要向操作系统额外的申请内存空间

现阶段，由于内存非常的便宜。所以写程序的时候，也不是特别的要考虑是否节省内存。微博，内存最大 196G

python内置方法sorted()和list.sort()排序

内置数据类型list的方法sort()，内置函数sorted() 这个的底层实现就是归并排序，只是使用了Python无法编写的底层实现，从而避免了Python本身附加的大量开销,速度比我们自己写的归并排序要快很多（10~20倍）,所以说我们一般排序都尽量使用sorted和sort

# Python内置函数sorted()
li = [random.randint(0,100000) for i in range(10000)]
start = time.time()
sorted(li)
print('sorted:%s' % (time.time() - start))

# python内置数据类型list.sort()
li = [random.randint(0,100000) for i in range(10000)]
start = time.time()
li.sort()
print('sorted:%s' % (time.time() - start))

'''
sorted:0.003000020980834961
sorted:0.003000020980834961
'''

冒泡排序

# 冒泡排序
# 最坏的时间复杂度是：（O(n^2)），最优的时间复杂度是：O(n)  有序的列表在内层循环一趟就就return了。
def bubble_sort(l):
    for i in range(len(l)-1):
        # 定一个标志位，做一个排序的优化。如果在循环第一趟的时候，
        # 发现列表是一个有序的列表，就不会走内层循环里面的if条件
        # 判断里面的代码，进行交换数字，flag标志位就不会被置换
        # 成False，进而走内层循环外面的if判断，终止整个函数的运行。

        flag = True
        for j in range(len(l)-i-1):
            if l[j] > l[j+1]:
                l[j],l[j+1] = l[j+1],l[j]
                flag = False
        if flag:
            return
# 冒泡排序
li = [random.randint(0,100000) for i in range(10000)]
start = time.time()
bubble_sort(li)
print('bubble_sort:%s' % (time.time() - start))


'''
bubble_sort:11.830676555633545
'''

选择排序

# 选择排序
def select_sort(l):
    for i in range(len(l)):
        minloc = i
        for j in range(i+1,len(l)):
            if l[j] < l[minloc]:
                l[j],l[minloc] = l[minloc],l[j]

# 选择排序
li = [random.randint(0,100000) for i in range(10000)]
start = time.time()
select_sort(li)
print('select_sort:%s' % (time.time() - start))

'''
select_sort:7.196411609649658
'''

插入排序

# 插入排序
# 时间复杂度 O(n^2)
def insert_sort(l):
    for i in range(1,len(l)):
        j = i-1
        temp = l[i]

        while j >= 0 and l[j] > temp:

            l[j+1] = l[j]
            j = j-1
        l[j+1] = temp

# l=[5,7,4,6,3,1,2,9,8]
# insert_sort(l)
# print(l)


# 插入排序
li = [random.randint(0,100000) for i in range(10000)]
start = time.time()
insert_sort(li)
print('insert_sort:%s' % (time.time() - start))

'''
insert_sort:6.566375494003296
'''

快速排序

def partition(l,left,right):
    tmp = l[left]
    while left < right:
        while left < right and l[right] >= tmp:
            right = right - 1
        l[left] = l[right]

        while left < right and l[left] <= tmp:
            left =left + 1
        l[right] = l[left]

    l[left] = tmp
    return left

#快速排序
# 时间复杂度：O(nlogn)
def quick_sort(l,left,right):
    if left < right:
        mid = partition(l,left,right)
        quick_sort(l,left,mid-1)
        quick_sort(l,mid+1,right)

# 快排
li = [random.randint(0,100000) for i in range(10000)]
start = time.time()
quick_sort(li, 0, len(li)-1)
print('quick_sort:%s' % (time.time() - start))

'''
quick_sort:0.03600168228149414
'''

希尔排序

# 希尔排序
'''
希尔排序是一种分组插入排序算法
首先取一个整数d1=n/2,将元素分为d1个组，魅族相邻元素之间的距离为d1,在各组内进行直接插入排序；
取第二个整数d2=d1/2，重复上述分组排序过程，直到d1=1，即所有元素在同一组内进行直接插入排序。
希尔排序每趟并不使某些元素有序，而是使整体数据越来越接近有序；最后一趟排序使得所有数据有序。
'''

def shell_sort(l):
    gap = len(l) // 2
    while gap > 0:
        for i in range(gap, len(l)):
            tmp = l[i]
            j = i - gap
            while j >= 0 and tmp < l[j]:
                l[j + gap] = l[j]
                j -= gap

            l[j + gap] = tmp
        gap //= 2
# 希尔排序
li = [random.randint(0,100000) for i in range(10000)]
start = time.time()
shell_sort(li)
print('shell_sort:%s' % (time.time() - start))

'''
shell_sort:0.06900382041931152
'''

计数排序

# 计数排序
def count_sort(l):
    n = len(l)
    res = [None] * n
    # 首次循环遍历, 每个列表的数都统计
    for i in range(n):
        # p 表示 a[i] 大于列表其他数 的次数
        p = 0
        # q 表示 等于 a[i] 的次数
        q = 0
        # 二次循环遍历, 列表中的每个数都和首次循环的数比较
        for j in range(n):
            if l[i] > l[j]:
                p += 1
            elif l[i] == l[j]:
                q += 1
        for k in range(p, p+q):  # q表示 相等的次数,就表示, 从 P 开始索引后, 连续 q 次,都是同样的 数
            res[k] = l[i]
    return res

# 计数排序
li = [random.randint(0,100000) for i in range(10000)]
start = time.time()
count_sort(li)
print('count_sort:%s' % (time.time() - start))

'''
count_sort:14.809847116470337
'''

归并排序

归并排序仍然是利用完全二叉树实现，它是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列。

基本过程：假设初始序列含有n个记录，则可以看成是n个有序的子序列，每个子序列的长度为1，然后两两归并，得到n/2个长度为2或1的有序子序列，再两两归并，最终得到一个长度为n的有序序列为止，这称为2路归并排序。

下面的截图来自《大话数据结构》相关章节，便于理解整个代码的实现过程。

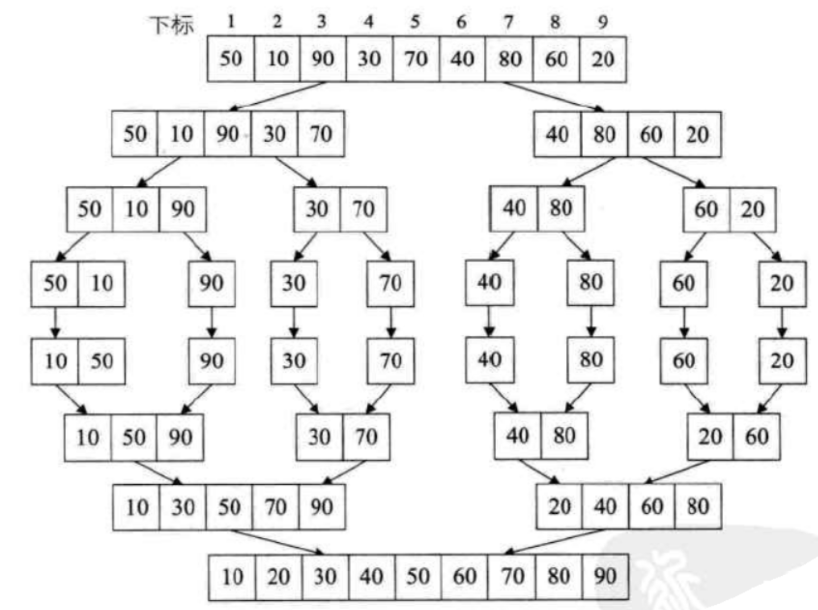
 图中主要表明了实例代码中的两部分，分别为原始序列的拆分和合并两部分。

# 归并排序
def merge_sort(lst):
    if len(lst) <= 1:
        return lst          # 从递归中返回长度为1的序列

    middle = len(lst) // 2
    left = merge_sort(lst[:middle])     # 通过不断递归，将原始序列拆分成n个小序列
    right = merge_sort(lst[middle:])
    return merge(left, right)

def merge(left, right):
    i, j = 0, 0
    result = []
    while i < len(left) and j < len(right):  # 比较传入的两个子序列，对两个子序列进行排序
        if left[i] <= right[j]:
            result.append(left[i])
            i += 1
        else:
            result.append(right[j])
            j += 1
    result.extend(left[i:])         # 将排好序的子序列合并
    result.extend(right[j:])
    return result

# 归并排序
li = [random.randint(0, 100000) for i in range(10000)]
start = time.time()
lst = merge_sort(li)
print("merge_sort:", time.time() - start)

'''
merge_sort: 0.06600356101989746
'''

列表查找

列表查找：从列表中查找指定元素

输入：列表、待查找元素

输出：元素下标或为查找到元素

顺序查找：

从列表的第一个元素开始，顺序进行搜索，直到找到为止。

二分查找：

从有序列表的候选区data[0:n]开始，通过对待查找的值与候选区中间值的比较，可以使候选区减少一半。

# 二分查找
def binary_search(l,low,high,value):
    mid = (low + high) // 2
    if low <= high:
        if l[mid] == value:
            return mid
        elif l[mid] > value:
            return binary_search(l,low,mid-1,value)
        else:
            return binary_search(l,mid+1,high,value)

    else:
        return "此数不存在！"

l = [1,2,3,4,5,6,7,8,9,10,11,12,13]
res = binary_search(l,0,len(l)-1,9)
print(res)

数据结构

malloc()到底如何申请内存空间？

转至：https://blog.csdn.net/m0_37631322/article/details/81777855

1.链表是什么

链表是一种上一个元素的引用指向下一个元素的存储结构，链表通过指针来连接元素与元素；

链表是线性表的一种，所谓的线性表包含顺序线性表和链表，顺序线性表是用数组实现的，在内存中有顺序排列，通过改变数组大小实现。而链表不是用顺序实现的，用指针实现，在内存中不连续。意思就是说，链表就是将一系列不连续的内存联系起来，将那种碎片内存进行合理的利用，解决空间的问题。

所以，链表允许插入和删除表上任意位置上的节点，但是不允许随即存取。链表有很多种不同的类型：单向链表、双向链表及循环链表。

2.单向链表

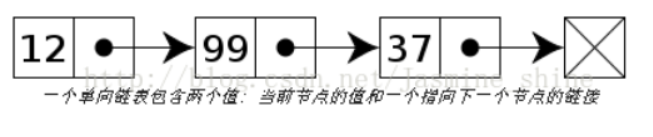
单向链表包含两个域，一个是信息域，一个是指针域。也就是单向链表的节点被分成两部分，一部分是保存或显示关于节点的信息，第二部分存储下一个节点的地址，而最后一个节点则指向一个空值。

3.双向链表

 从上图可以很清晰的看出，每个节点有2个链接，一个是指向前一个节点（当此链接为第一个链接时，指向的是空值或空列表），另一个则指向后一个节点（当此链接为最后一个链接时，指向的是空值或空列表）。意思就是说双向链表有2个指针，一个是指向前一个节点的指针，另一个则指向后一个节点的指针。

4.循环链表

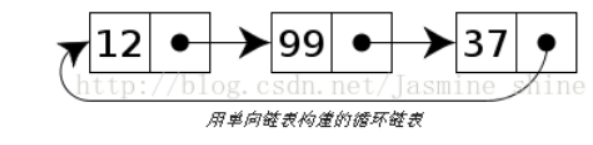
循环链表就是首节点和末节点被连接在一起。循环链表中第一个节点之前就是最后一个节点，反之亦然。

5.数组和链表的区别？

不同：链表是链式的存储结构；数组是顺序的存储结构。

链表通过指针来连接元素与元素，数组则是把所有元素按次序依次存储。

链表的插入删除元素相对数组较为简单，不需要移动元素，且较为容易实现长度扩充，但是寻找某个元素较为困难；

数组寻找某个元素较为简单，但插入与删除比较复杂，由于最大长度需要再编程一开始时指定，故当达到最大长度时，扩充长度不如链表方便。 相同：两种结构均可实现数据的顺序存储，构造出来的模型呈线性结构。

6.链表的应用、代码实践

约瑟夫问题：

传说在公园1世纪的犹太战争中，犹太约瑟夫是公元一世纪著名的历史学家。在罗马人占领乔塔帕特后，39 个犹太人与约瑟夫及他的朋友躲到一个洞中，39个犹太人决定宁愿死也不要被敌人俘虏，于是决定了一个流传千古的自杀方式，41个人排成一个圆圈，由第1个人开始报数，每报到第3人该人就必须自杀，然后再由下一个人重新报数，直到所有人都自杀身亡为止。然而约瑟夫和他的朋友并不想遵从这个约定，约瑟夫要他的朋友先假装遵从，他将朋友与自己安排在第个和第 个位置，于是逃过了这场死亡游戏,你知道安排在了第几个嘛？

针对以上问题，使用单向循环链表的方式求解：

# 控制参数：
nums = 41
call = 3
# 参数定义：
peoples = [True for _ in range(nums)]

# append的方法性能不好
# for _ in range(nums):
#    peoples.append(True)

result = []
num = 1

while (any(peoples)):
    for index, people in enumerate(peoples):
        if people:
            if num == call:
                peoples[index] = False
                result.append(index + 1)
                #                print(index+1)#每轮的出局者
                #                print(peoples)#每次的队列状态
                num = 1
            else:
                num += 1

print('
总数为%d,报数为%d' % (nums, call))
print('约瑟夫序列为：
%s
' % result)

7.自我理解

1）数组便于查询和修改，但是不方便新增和删除

2）链表适合新增和删除，但是不适合查询，根据业务情况使用合适的数据结构和算法是在大数据量和高并发时必须要考虑的问题

栈和队列的应用

栈

是一种可以实现“先进后出”的存储结构

类似于一个箱子，先放进去的书，最后才能取出来，后放进去的书，先去出来。因为在栈中永远只能先操作栈顶的元素。对栈顶的元素进行push和pop。

函数调用在栈中的应用

函数在调用的时候会在内存中开辟一块栈空间，在调用一个函数的时候，会将这个函数压入我们申请的栈内，如果此时调用的还有其他函数，按照“先调用后返回”的原则，先入栈（push）的这个函数会将函数执行的控制权交给后入栈（push）的函数，依次类推，将这些函数压入栈中，直到将执行函数的控制权交给栈顶的那个函数。栈顶的那个函数执行完之后，会出栈（pop），然后将函数的控制权交给当前栈顶的元素（函数），依次出栈，直到程序判断栈空，所有代码执行完毕。

队列

是一种可以实现“先进先出”的存储结构。

类似于一个管道，先入管道的，先从管道出来。

应用：生产者消费者模型（起源于操作系统）