疯狂%%%几个月前就秒了此题的Tyher巨佬
借着这题总结一下决策单调性优化DP吧。蒟蒻觉得用数形结合的思想能够轻松地理解它。
首先,题目要我们求所有的(p_i),那么把式子变一下
绝对值看着很不爽,我们把它拆开
单独看前一部分
很明显是个要用决策单调性优化的式子。把序列翻转以后,后一部分的算法和前面是一样的,所以只讨论前一部分了。
对于每个(j),把(a_j+sqrt{i-j})看成关于(i)的函数(f_j)。我们要做的就是在所有(jleq i)的函数中找到最值。比如样例:
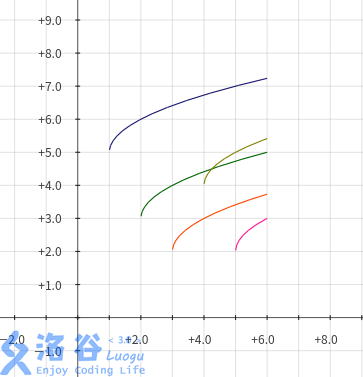
观察发现,真正有用的函数只有最上面那个!然而实际情况比这个稍复杂些。sqrt的增速是递减的,因此可能存在一个(j)比较小的函数,在某一时刻被(j)比较大的函数反超。我们大概需要维护这样的若干个函数:
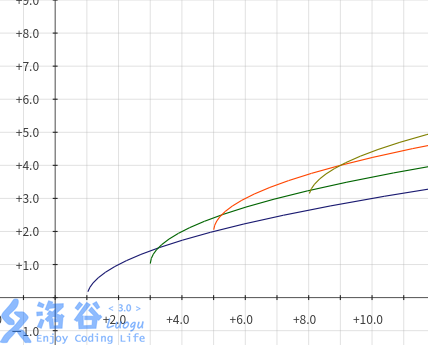
我们用队列实现决策二分栈(不懂的可以参考一下蒟蒻的blog),按(j)从小到大依次维护这些函数。显然,对于其中任意两个相邻的函数(f_t,f_{t+1}),它们都有一个临界值(k_{t,t+1})。显然序列中的(k_{1,2},k_{2,3}...)也要严格递增。否则,如果(k_{t,t+1}ge k_{t+1,t+2}),可以想象(f_{t+1})根本没有用。
先for一遍(i),我们尝试着把(f_i)加入队列。这时候为了保证(k)递增,设队尾决策为(t),我们判断,如果(k_{t-1,t}ge k_{t,i})(此时会有(f_t(k_{t-1,t})le f_i(k_{t-1,t}))),那么(t)没用,出队。
该出去的都出去后,(i)就可以加入队尾了。这时候可以来求(p_i)了。我们检查一下队首决策(h),如果(t_{h,h+1}le i),说明(h)的巅峰时刻已经过去,出队。最后队首就是所有函数中的最大值。
貌似并没有用到什么三元组啊qwq
update:感谢孤独·粲泽的指正,二分上下界确实该调调
不过还是没有用到什么三元组啊qwq,蒟蒻之前都把临界值(k)存下了,直接用就可以啦
#include<bits/stdc++.h>
#define RG register
#define R RG int
#define G if(++ip==iend)fread(ip=buf,1,N,stdin)
#define calc(i,j) a[j]+sq[i-j]//计算函数值
using namespace std;
const int N=5e5+9;
char buf[N],*iend=buf+N,*ip=iend-1;
int n,a[N],q[N],k[N];
double p[N],sq[N];
inline int in(){
G;while(*ip<'-')G;
R x=*ip&15;G;
while(*ip>'-'){x*=10;x+=*ip&15;G;}
return x;
}
inline void chkmx(RG double&x,RG double y){
if(x<y)x=y;
}
inline int bound(R x,R y){//二分临界值k
R l=y,r=k[x]?k[x]:n,m,ret=r+1;//控制二分上下界
while(l<=r){
m=(l+r)>>1;
if(calc(m,x)<=calc(m,y))
ret=m,r=m-1;
else l=m+1;
}
return ret;
}
void work(){
for(R h=1,t=0,i=1;i<=n;++i){
while(h<t&&calc(k[t-1],q[t])<calc(k[t-1],i))--t;//维护k单调
k[t]=bound(q[t],i);q[++t]=i;
while(h<t&&k[h]<=i)++h;//将已经不优的决策出队
chkmx(p[i],calc(i,q[h]));//因为做两遍所以取max
}
}
int main(){
n=in();
R i,j;
for(i=1;i<=n;++i)
a[i]=in(),sq[i]=sqrt(i);
work();
for(i=1,j=n;i<j;++i,--j)//序列翻转
swap(a[i],a[j]),swap(p[i],p[j]);
work();
for(R i=n;i;--i)//翻转过了所以要倒着输出
printf("%d
",max((int)ceil(p[i])-a[i],0));
return 0;
}