【剑指Offer-循环和递归】面试题10.4：矩形覆盖

题目描述

我们可以用2x1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2x1的小矩形无重叠地覆盖一个2xn的大矩形，总共有多少种方法？

思路

可以推一下：用2x1的小矩形覆盖2x1的大矩形共1种方法，覆盖2x2的矩形共2种方法，覆盖2x3的矩形共3种方法，覆盖2x4的矩形共5种方法，可以看出方法数满足斐波那契数列。

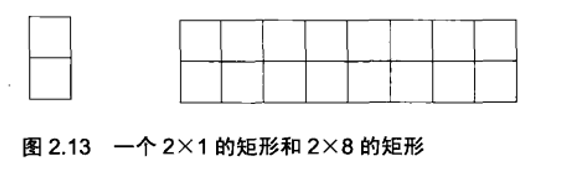
如上图所示，把使用2x1的矩形覆盖2x8的矩形的放法数记为f(8)，则用第一个2x1的矩形覆盖时有两种放法：（1）竖着放，此时右边剩下2x7的区域，所以放法数还剩f(7)；（2）横着放，此时左下角必须再横着放一个2x1的矩形，此时还剩下2x6的区域，所以剩余放法数f(6)，所以f(8)=f(7)+f(6)。
代码如下：

class Solution {
public:
    int rectCover(int number) {
        if(number<1)
            return 0;
        
        int a[2];
        a[0] = 1;
        a[1] = 2;
        if(number<=2)
            return a[number-1];
        
        for(int i=2; i<number; i++){
            int t = a[0] + a[1];
            a[0] = a[1];
            a[1] = t;
        }
        return a[1];
    }
};