我们把模型在在训练集上的误差叫做训练误差,在新样本的误差叫做泛化误差。我们希望模型的训练误差和泛化误差都比较小。在实际使用中,我们使用测试集来模拟新样本,并使用模型在测试集上的误差来作为泛化误差的近似。测试集是不参与训练过程的,而训练模型可以有不同的方法,例如使用不同的模型、不同的参数,如何选择合适的模型呢?
为了选择合适的模型,我们可以将训练数据划分为两部分,一部分作为训练模型使用的训练集,另一部分作为验证集,验证集用来评估模型的性能,验证集的结果可以帮助调参或者修改模型结构。我们以验证集的结果为标准就可以选出合适的模型。常用的数据划分方法有:留出法(hold-out)、交叉验证法(cross validation)、留一法(Leave-One-Out,LOO)和自助法(boostraping)。
留出法
留出法(hold-out)直接将数据集(D)划分为两个互斥的集合,一个作为训练集 (S),另一个作为验证集 (T),也就是 (D = Scup T),(Scap T=varnothing)。例如数据集 (D) 中包含 1000 个样例,其中有 500 个正例,500 个反例。我们可以使用 7:3 的比例将其划分为训练集 (S) 以及验证集 (T),这样 (S) 中有 700 个样本,(T) 中有 300 个样本。在划分的过程中,要尽可能地保证 (S) 和 (T) 中的正例反例比例相同(也就是数据分布相同,可以使用分层抽样),例如 (S) 中 700 个样本有 350 个正例和 350 个反例,(T) 中有 150 个正例和 150 个反例,(S) 和 (T) 中正反例的比例均为 1:1.
当确定了训练集和验证集的比例后,也有多种进行划分的方法(例如不同的随机数种子就会得到不同的划分结果)。为了结果的稳定性,我们可以进行 n 次随机划分,然后将这 n 次随机划分实验结果的平均值作为最终的实验结果(我们将一次训练测试的过程称为一次实验)。
交叉验证法
交叉验证法(cross validation)首先将数据集划分为 k 个互斥的集合,然后进行 k 次实验,每次选择其中一个不同于其他次的集合作为验证集,剩余的 k-1 个集合作为训练集,将 k 次实验结果的平均作为最终的实验结果。数据集被划分成 k 个互斥集合的交叉验证方法被称为k折交叉验证,常用的 k 值有 5、10、20等。下图是 10 折交叉验证的示意图:
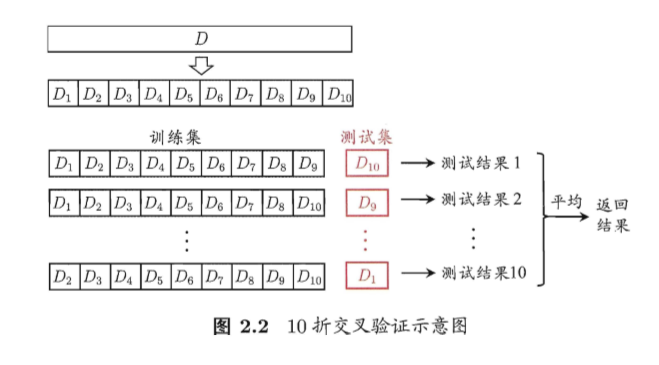
假设我们确定了折数 k,由于进行划分的方法不同,得到的结果也会不同(例如使用不同的随机数种子)。在实际使用中,我们可以进行 p 次不同的 k 折交叉验证,取 p*k 次实验结果的平均作为最终的实验结果,这叫做p次k折交叉验证。例如,10次10折交叉验证共进行了100次实验。
留一法
留一法(Leave-One-Out,LOO)可以看做是交叉验证法的一个特例。假设数据集 (D) 中有 m 个样例,我们将其划分为 m 个互斥的集合进行交叉验证,这种交叉验证方法就被成为留一法。在留一法中,我们每次使用 m-1 个样例进行训练,1 个样例进行测试。这样用训练出的模型和直接使用全部数据集 (D) 训练出的模型非常接近,但当数据量比较大时,例如数据集包含 100 万个样例,使用留一法意味着我们要训练 100 万个模型,这显然是不现实的。
自助法
我们希望使用整个训练集 (D) 来训练模型,但留出法、交叉验证法只使用了一部分,留一法的复杂度又太高。这时我们可以通过自助法(bootstraping)来减少样本规模不同带来的影响以及高效地进行实验。
留出法每次从数据集 (D) 中抽取一个样本加入数据集 (D^{prime}) 中,然后再将该样本放回到原数据集 (D) 中,也就是说 (D) 中的样本可以被重复抽取。这样,(D) 中的一部分样本会被多次抽到,而另一部分样本从未被抽到。假设抽取 m 次,则在 m 次抽样中都没有被抽到的概率为 ((1-frac{1}{m})^m),取极限有

也就是说,原数据集 (D) 中约 36.8% 的数据未在 (D^{prime}) 中出现过,所以我们可以将 (D^{prime}) 作为训练集,将 (D-D^{prime})((D) 与 (D^{prime}) 的差集)作为验证集。
自助法适用于数据集较小,难以划分训练、验证集的情况。
参考
1、周志华《机器学习》