题目描述
给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。
说明:不允许修改给定的链表。
示例:
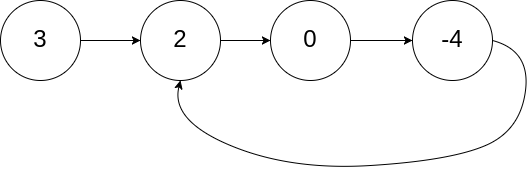
输入:head = [3,2,0,-4], pos = 1
输出:tail connects to node index 1
解释:链表中有一个环,其尾部连接到第二个节点。

输入:head = [1], pos = -1
输出:no cycle
解释:链表中没有环。
题目描述: https://leetcode-cn.com/problems/linked-list-cycle-ii/
思路
使用两个指针 slow 和 fast 来做:
- slow 每次走一步,fast 每次走两步,如果 slow == fast,则说明 slow 和 fast 在环中相遇;
- 将 fast 放回链表头(fast = head),然后 slow 和 fast 每次都走一步,当 slow 和 fast 相等时,说明此时 slow 或者 fast 就是链表环的入口节点。
证明:
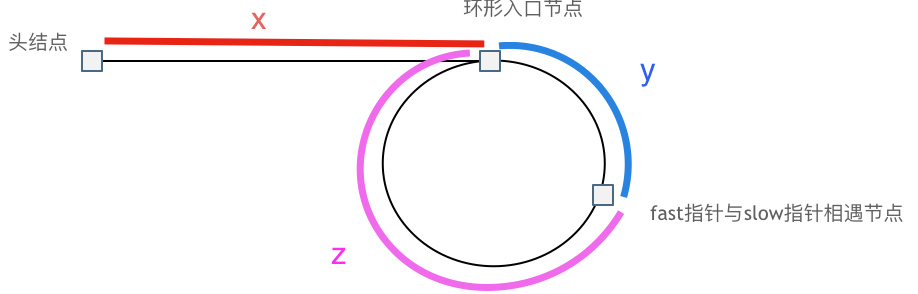
如上图所示,假设头节点到环入口节点的距离为 x,环入口节点到 slow 和 fast 相遇点的距离为 y,slow 和 fast 相遇点到环入口节点的距离为 z,则 slow 走的路程为 x + y,而 fast 走的路程为 x + y + n(y + z)也就是 fast 在环中绕了 n 圈后才与 slow 相遇(n≥0)。因为 fast 每次走 2 步,slow 每次走 1 步,所以相遇时 fast 走的路程是 slow 的两倍,也就是
[2(x+y)=x+y+n(y+z)
]
因为我们要求的是 x,所以整理可得
[x=n(y+z)-y = (n-1)(y+z)+z, ~~ n ge 1
]
上式有两种情况:
- n==1 时,x==z,此时我们将 fast 放到链表头,然后 fast 和 slow 每次走一步,相遇节点就是环的入口;
- n>1 时,我们将 fast 放到链表头,当 fast 和 slow 相遇时,说明 slow 在环里转了 n-1 圈后又走了 z 步,等价于 n==1 的情况。
代码如下:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
if(head==NULL) return head;
ListNode* slow = head;
ListNode* fast = head;
while(fast!=NULL && fast->next!=NULL){
slow = slow->next;
fast = fast->next->next;
if(slow==fast) break;
}
if(fast==NULL || fast->next==NULL) return NULL; // 注意这个条件
fast = head;
while(slow!=fast){
slow = slow->next;
fast = fast->next;
}
return slow;
}
};