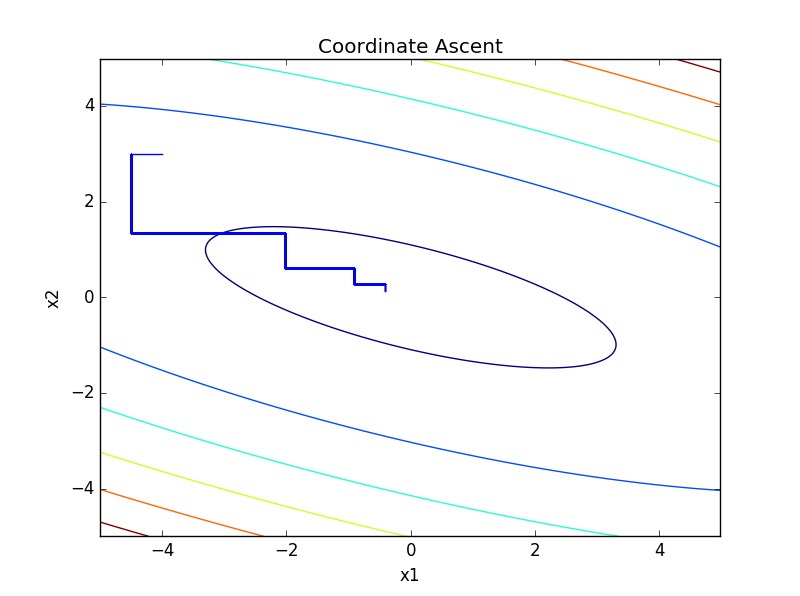
原理
对于没有约束限制的优化问题,可以每次仅更新函数中的一维,固定其他参数,迭代多次以达到求解优化函数的目的。
具体过程如下
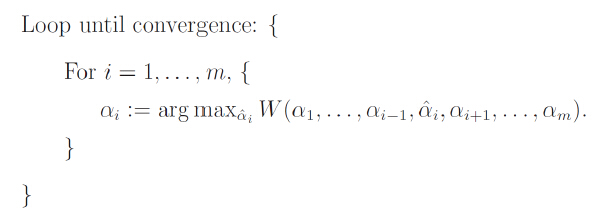
举例
求解问题 f(x1,x2) = 3x12 + x22 + 4x1x2 - 8
迭代次数计数
{
1、固定x2更新x1 x1 = - 2/3 x22、固定x1更新x2 x2 = -2 x1}# -*- coding: utf-8 -*- """ Created on Wed Apr 05 18:09:41 2017 @author: LoveDMR 坐标上升法 """ import numpy as np import matplotlib.pyplot as plt delta = 0.025 x1 = np.arange( -5 , 5 , delta ) x2 = np.arange( -5 , 5 , delta ) X1 , X2 = np.meshgrid( x1 , x2 ) Y = X1**2 + 5 * X2**2 + 3 * X1 * X2 - 6 plt.figure() bg_fig = plt.contour(X1,X2,Y) a , b = [] , [] a.append(-4) b.append(3) j = 1 for i in xrange(1,150): a_tmp = - 1.5 * b[j-1] a.append( a_tmp ) b.append( b[j-1] ) j = j + 1 b_tmp = - 0.3 * a[j-1] b.append( b_tmp ) a.append( a[j-1] ) plt.plot(a , b) plt.title( "Coordinate Ascent" ) plt.xlabel('x1') plt.ylabel('x2') plt.show()
另外可以迭代到W的值不再变化或着变化幅度小于某个值即可