写在前面:
魔鬼课程oo第一单元终于结束,当终究要落笔总结,竟不知从何写起……
回首再去看第一次的作业,你会满足于那时的幸福,或许,这就是成长吧!
千言万语,一切尽在无言中……
知识点总结:
-
对象,类
-
面向对象的编程思想
-
-
接口
-
重写
-
……
作业代码思路:
本单元的三次作业是一个层层深入的关系,我认为,虽然“推倒重来”式写法十分不可取,但对于一个刚刚接触面向对象思想的新手来说,也可能是不可少的一个环节,我们能从自己推倒重来的过程中,逐渐领悟面向对象的封装等特点,我们在吸取自己教训的同时也能得到锻炼。或者说,至少我们知道这样做是不对的,怎样做是好的,前面没有打好基础,产生的苦果到后面都是自己尝。
第三次作业的框架相较于前两次作业来说更为完整,我对第三次作业理解也更为深刻,因此,首先从第三次作业讲起。
第三次作业
如上图所示,这是我第三次作业的代码结构。
(I代表接口Interface;m代表方法method)
在本次作业中我将因子共分为三类,常数因子(Constant)、三角函数因子(Tri)、表达式因子(Poly),三种因子均继承自父类Factor。在三种因子中,均存在求导方法(derivation),我们将其封装为一个接口derivation。
1.程序入口为main函数,在main函数中我们创建一个Regexp类型的对象;
2.在Regexp中,需要完成简单的格式检查和简单的正则表达式化简。
-
具体来说我将格式检查分为三部分,分别为检查是否有非法字符(checkIllegal)、是否有由空白符导致的错误(checkSpace)、是否有括号匹配错误(checkBracket)、是否有连运算符导致的错误(checkMultiOp)
-
正则表达式化简,也叫做预处理,我在思考许多情况后认为化简后带来的问题不少于化简带来的便利,因而我在最终的预处理过程中只处理了空白符,即删掉所有空白符。
3.由于本次作业中表达式本身也可以作为因子(即表达式因子),表达式内部可以嵌套,我们对表达式进行求导,可直接在当前输入字符串开始和结束加入左括号和右括号,将其形象为一个表达式因子,之后套用表达式因子的求导方法,即进入Poly中处理。
4.此次作业最大的挑战便是没有跳出可以嵌套的坑,以往的作业都是先使用大正则检测是否格式错误,然后通过加号分割每一“项”。但这次包含嵌套后,我无法做到大正则检测(当然这种做法本身就不是很好的做法),于是这次我尝试了一种船新玩法,边匹配,边检测格式,边计算。
-
具体来说,为三类因子构造自己的正则表达式。之后从头开始遍历,找到对应的因子后交于对应的类中去处理
-
通过运算符来分割:+或-号代表一项结束,开始下一项;*号代表下一个仍是因子,他们属于同一项。
-
当一项没有结束时,只生成对应的因子;
-
当一项结束后,开始根据链式求导法则对此项求导,求导的结果保存到一个字符串中(ans)
不足:没有化简(或者说,只有十分简单的化简)
分析第三次作业的耦合内聚情况


容易看出,在第三次作业中,我的代码仍存在很大问题,方法和类的耦合度太高,这样的弊端就是容易牵一发而动全身,真正的优秀代码应该是每一部分都是完美封装好的。
具体分析来看,代码的耦合主要集中在Poly和Tri两个类上。不难理解,因为我只将因子分为4类,也就是三角函数中有嵌套的也归为了三角函数因子这类,我认为这样做的好处在于减少因子分类情况,但缺点在于需要在三角函数Tri和多项式Poly类之间来回切换调用,因而造成耦合度较高。
第二次作业:

第二次作业和第一次作业做法相似(所以才导致我刚看到第三次作业时觉得无从下手)
1.程序主入口main函数,构建Regexp对象
2.在Regexp类中,完成格式检查和预处理工作,具体来说
-
首先检查由空白字符引起的错误,没有问题后删除所有空白字符
-
构建正则表达式,字符串匹配
-
第二步匹配成功后化简表达式
-
通过+号将每一项进行分割(在第三步基础上保证每两项之间通过+号分割,且只有两项之间有加号)
-
将每一项push到Map数组中,已存在则在此基础上相加,否则新生成一个对象
3.在Map类中,将每一项存好后开始计算导数,计算导数的过程也较为简单,由于Map类中每个对象包含四个属性,分别为系数、三个因子的指数,所以根据链式求导法则进行求导即可。
分析第二次作业耦合内聚情况:
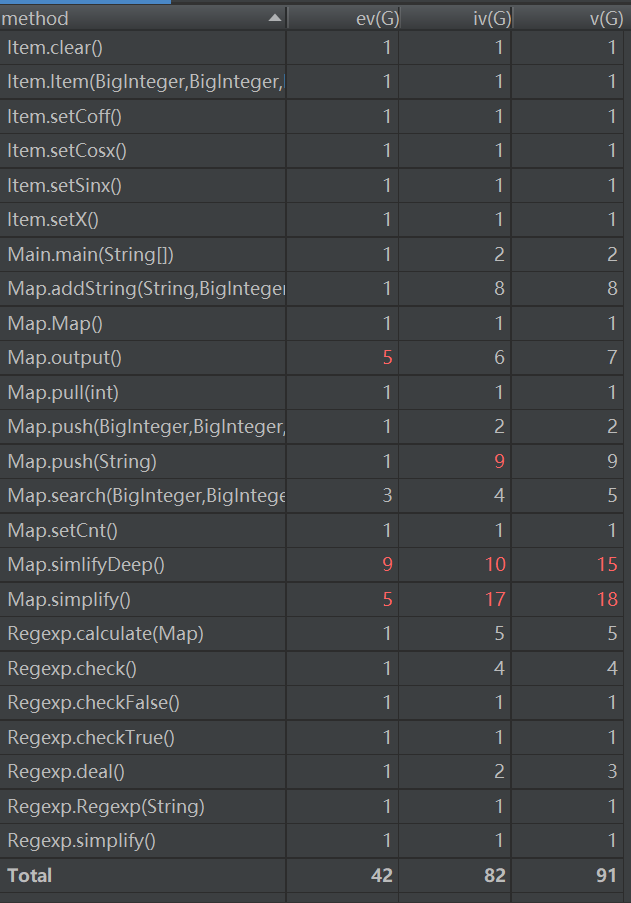

第二次作业我的map类中的化简方法耦合度较高,所有的问题全部集中在了Map这个类当中,而我出bug的点也是在化简这里。原因在于我对表达式的化简没有一个很好的策略,没有如何精妙的构思,也没有将贪心算法用到化简当中(虽然贪心确实存在一些问题),简单的遍历使得复杂度增加,而且还易错。
第一次作业
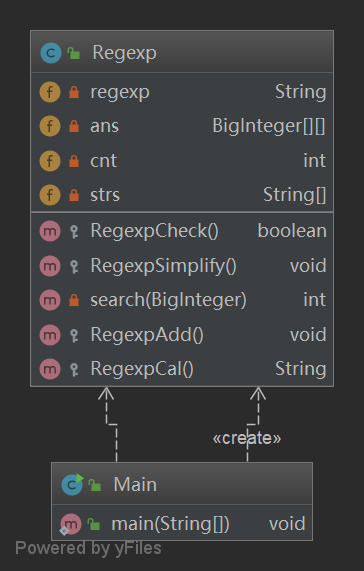
第一次作业较为简单,一共就构建了两个类。
1.程序入口main函数,构建Regexp对象
2.在Regexp类中,进行格式检查和化简工作,然后计算求导
分析第一次作业耦合内聚情况:
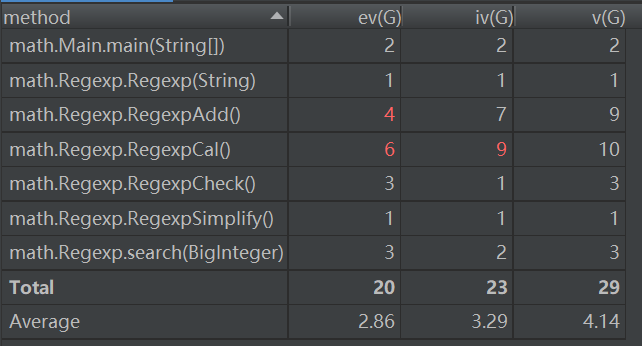

可能有人会很惊讶,第一次作业这么简单怎么还会有代码问题呢?第一次作业更多有点像面向过程,所有的方法都集中在了Regexp类当中,也无疑Regexp的耦合度最高了……
攻击和防御(bug)
互测环节真的是惊险不断,仍无法忘记第二次作业翻车进入C组时候的惨烈情况,地地道道做了回狼人,心里愧疚不已……当时虽然已知是板上钉钉的事,可心里仍不愿意接受这个事实(谁的心中没有“万一“这种侥幸心理呢?)
我的攻击方法:
1.读别人的正则表达式部分,分析他是否有没有考虑到的情况,比如某个地方少判断空格或者带符号数前面的符号
2.通读代码,定点爆破。不要求通读一遍后十分理解作者的思路,因为我认为这是一个十分复杂的过程,而且每个人脑海中也有一套自己的正确做法,所以只是对他代码中某些觉得奇怪或者觉得这样写容易出错的地方定点爆破,检测是否真的在这里出错即可。
3.对拍,遍地开花。大面积构造多种数据,通过python或者shell脚本对比不同程序运行的结果。当通过这种方法找到对方bug后不是急于高兴,而是分析他为什么有此错误。这样做的目的不是为了可以在一个错误上构造多个bug进行攻击,因为多次提交同质bug实在是费力不讨好的事,因此恰恰相反,我们的目的是在于之后的对拍中避免此类同质bug的出现,同时在分析他代码问题的时候对自己也是种提升。
4.总之,寻找bug和逻辑漏洞是相互关联的两部分,我们通过寻找到的bug可以反过来分析他的代码漏洞;另一方面,我们通过分析出的代码漏洞可以构造相应的bug数据。
我的防御方法:
1.分析代码逻辑,反复读自己代码,反复理自己的代码逻辑,分析是否有逻辑漏洞。
2.构造数据检测错误。
自己出现的bug:
第一次作业:无
第二次作业:强测出现三个bug,互测阶段出现一个bug。
强测bug1:2*x-x+sin(x)*cos(x)
强测bug2:1*sin(x)^1*cos(x)^1*x^1+0*cos(x)^0*sin(x)^0*x^0+-1*x^-1*cos(x)^-1*sin(x)^-1+x^-1+sin(x)^-1+cos(x)^1
强测bug3:+++1*1*1*x*sin(x)^233*cos(x)^2+cos(x)^6*x^-1*sin(x)^233-- -4*4*sin(x)^233*x^9*cos(x)^4
互测bug:s i n(x)
第三次作业:互测出现两个bug
互测bug1:-sin(x)^+3*cos(x)
互测bug2:sin(((x)- - (x)))^+8
bug分析:
第二次作业的强测三组bug均是由于化简出现的问题,我的做法是在生成字符串答案之后再通过正则匹配进行化简,由此出现了很大问题,因为存在情况没有考虑完整。
互测出现的bug是非常简单的情况,由于空格问题没有考虑全面,导致正则表达式匹配漏掉了情况。
第三次作业互测出现的两个bug全都是因为正则表达式漏掉了情况,在匹配三角函数因子时,正则表达式中没有体现出带符号整数前面的符号。
综合分析,第二次作业和第一次作业相比多了些复杂度,我在化简结果表达式时没有将问题考虑全面,导致强测爆炸(一直跌到了C组)……其他小问题都是在正则表达式格式判断处出现的问题,这也和我攻防的手段几近相同,确实是在正则表达式处容易出问题。
第三次作业不允许检查格式错误,我认为有利有弊,当然从我的视角来看也增大了找别人bug的难度,要求我们更认真的去找出别人的逻辑错误……
Applying Creational Pattern
前两次作业对面向对象思想体会不深,尤其是第一次作业,几乎就是按照面向过程莽下来的。到第二次时其实我们好多人已经猜到第三次作业会有嵌套的情况了,但自己当时还是偷懒了些,没有很好的将接口、继承运用到程序中来简化之后的工作。直到第三次作业,我觉得自己的代码就是个浴火重生的过程,因为之前两次作业的好多东西都不能再用了,包括思路都完全不同,在这次作业中,我运用继承来定义类之间的关系,定义接口来封装求导方法……
工厂模式是一种很常用的实例化对象模式,是指用工厂方法代替new操作的一种模式,它具有更大的可扩展性和尽量少的修改量。在工厂模式中,我们在创建对象时不会对客户端暴露创建逻辑,并且是通过使用一个共同的接口来指向新创建的对象。
总结
通过第一单元的这三次作业,我逐渐从面向过程向面向对象转变,不止掌握了Java一些基本语法和漂亮的代码风格,更重要的是掌握面向对象的编程思想。继承,封装,接口……这些概念在脑海中一遍又一遍地闪过,希望日后能更加熟练的运用面向对象思想解决问题!
