1)世界变换
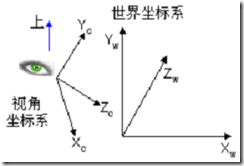
我们在建立三维实体的数学模型时,通常以实体的某一点为坐标原点,比如一个球体,很自然就用球心做原点,这样构成的坐标系称为本地坐标系(Local Coordinates)。实体总是位于某个场景(World Space)中,而场景采用世界坐标系(World Coordinates),如图所示,因此需要把实体的本地坐标变换成世界坐标,这个变换被称为世界变换(World Transformation)。
屏幕剪辑的捕获时间: 2007/6/22, 15:58
在Direct3D中,坐标变换通过一个4X4矩阵来实现,对于世界变换,只要给出实体在场景中的位置信息,就可以借助Direct3D函数得到变换矩阵,具体计算步骤如下:
- 首先把实体旋转在世界坐标系的原点,使两个坐标系重合;
- 在世界空间中,对实体进行平等移动,其对应的平移变换阵TT可由函数D3DXMatrixTranslation求得;
- 把平移后的实体沿自身的Z轴旋转一个角度(角度大于0,表示从Z轴的正向朝原点看上去,旋转方向为顺时针;反之为逆时针,下同),对应的旋转变换阵TZ用D3DXMatrixRotationZ计算;
- 把实体沿自身的Y轴旋转一个角度,用D3DXMatrixRotationY求出变换阵TY;
- 把实体沿自身的Y轴旋转一个角度,用D3DXMatrixRotationX求出变换阵TX;
- 最后对实体进行缩放,假设三个轴的缩放系数分别为SX、SY、SZ,该操作对应的变换阵TS可由函数D3DXMatrixScaling求得;
- 最终的世界变换矩阵TW=TS·TX·TY·TZ·TT,在Direct3D中,矩阵乘法用函数D3DXMatrixMultiply实现,注意相乘顺序为操作的逆序。
从以上描述中,我们很容易得出:实体的运动可以通过不断的改变世界变换矩阵来实现。
2)视角变换
实体确定后,接下来确定观察者在世界坐标系中的方位,换句话说,就是在世界坐标系中如何放置摄像机.观察者(摄像机)所看到的景象,就是Direct3D窗口显示的内容.
确定观察者需要三个量:
- 观察者的点坐标;
- 视线方向,为一个矢量,不过Direct3D用视线上的一个点来替代,此时视线方向就是从观察者指向该目标点,这样表示更直观一些;
- 上方向,通俗地说,就是观察者的头顶方向,用一个矢量表示.
确定后,以观察者为原点,视线为Z轴,上方向或它的一个分量为Y轴(X轴可由左手法则得出,为右方向),构成了视角坐标系,如下图所示.我们需要把实体从世界空间转换到视角空间,这个坐标变换被称为视角变换(View Transformation).
屏幕剪辑的捕获时间: 2007/6/22, 20:56
与世界变换相比,视角变换矩阵的获取要容易得多,只需调用一个函数D3DXMatrixLookAtLH,其输入参数就是决定观察者的那三个量.
3)投影变换
实体转换到视角空间后,还要经过投影变换(Projection Transformation)三维的实体才能显示在二维的计算机屏幕上.
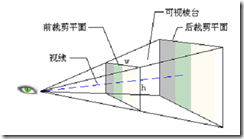
Direct3D使用透视投影变换(Perspective Transformation),此时在视角空间中,可视区域是一个以视线为轴心的棱台(Viewing Frustum),如下图所示.想象一下你处在一个伸手不见五指的房间里,面前有一扇窗户,你可以透过窗户看到各种景物.窗户就是棱台的前裁剪平面,天空、远山等背景是后裁剪平面,期间的可视范围是景深。投影变换把位于可视棱台内的景物投影到前裁剪平面,其间的可视范围是景深。投影变换把位于可视棱台内的景物投影到前裁剪平面,由于采用透视投影,距离观察者远的对象会变小,从而更具有真实感。在Direct3D中,前裁剪平面被映射到程序窗口,最终形成了我们在屏幕上版的画面。
屏幕剪辑的捕获时间: 2007/6/22, 21:10
透视投影变换由四个量决定:
- 前裁剪平面的宽度W;
- 前裁剪平面的高度H;
- 前裁剪平面到原点的距离Z1;
- 后裁剪平面到原点的距离Z2。
由于W、H用起来不是很直观,因此实际应用中,常用fov和aspect代替W、H,其中fov是Y方向上的可视角度,通常取π/4;aspect是前裁剪平面的高度与宽度之比,通常取1(由三角函数定义,易知H=2·z1·tg(fov/2),W=H/aspect)。用这四个量来调用函数D3DXMatrixPerspectiveFovLH,即可获得投影变换矩阵。
得到三个变换矩阵后,还需要调用方法 IDirect3DDevice9::SetTransform把它们设置到渲染环境中。
最后,可以用三句话来概括这些变换的作用:世界变换决定实体的位置;视角变换决定观察者的位置;投影变换决定观察者的可视区域。