重建二叉树

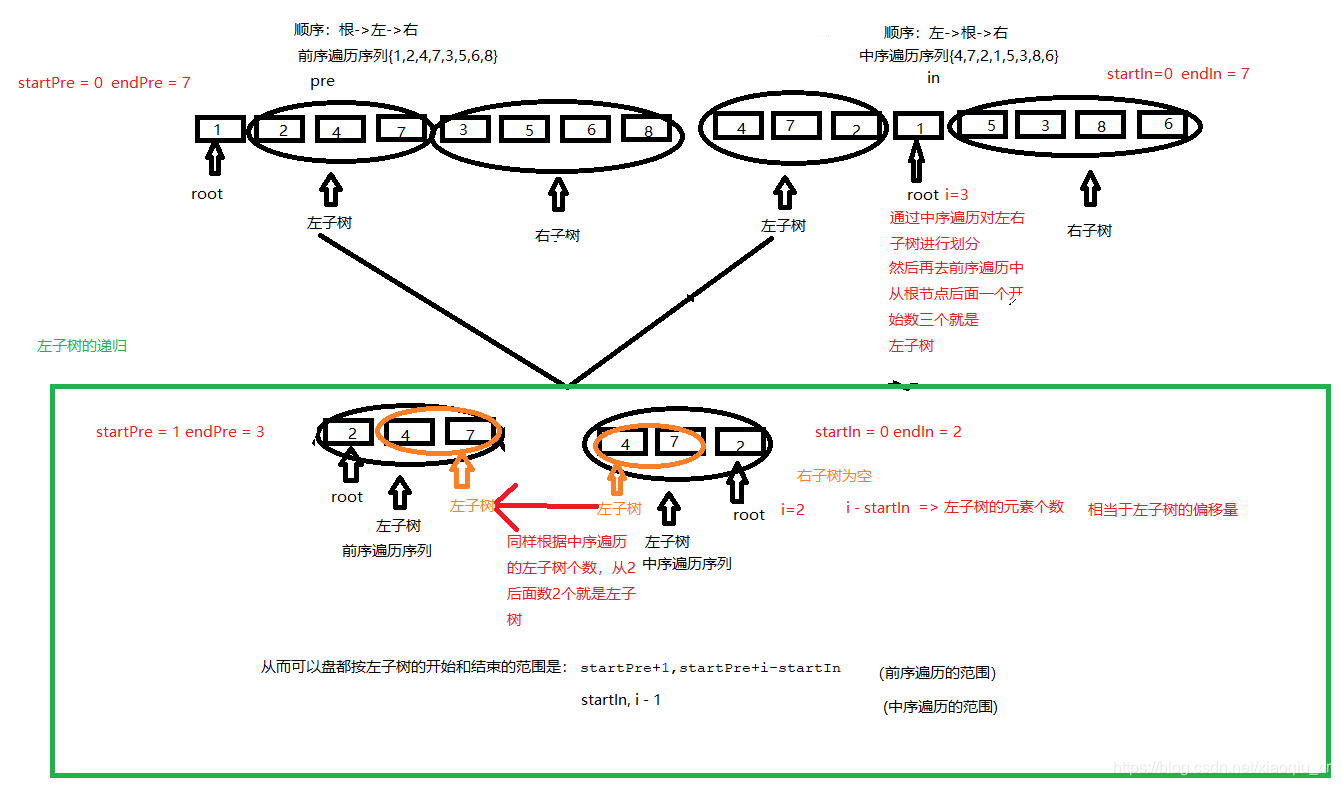
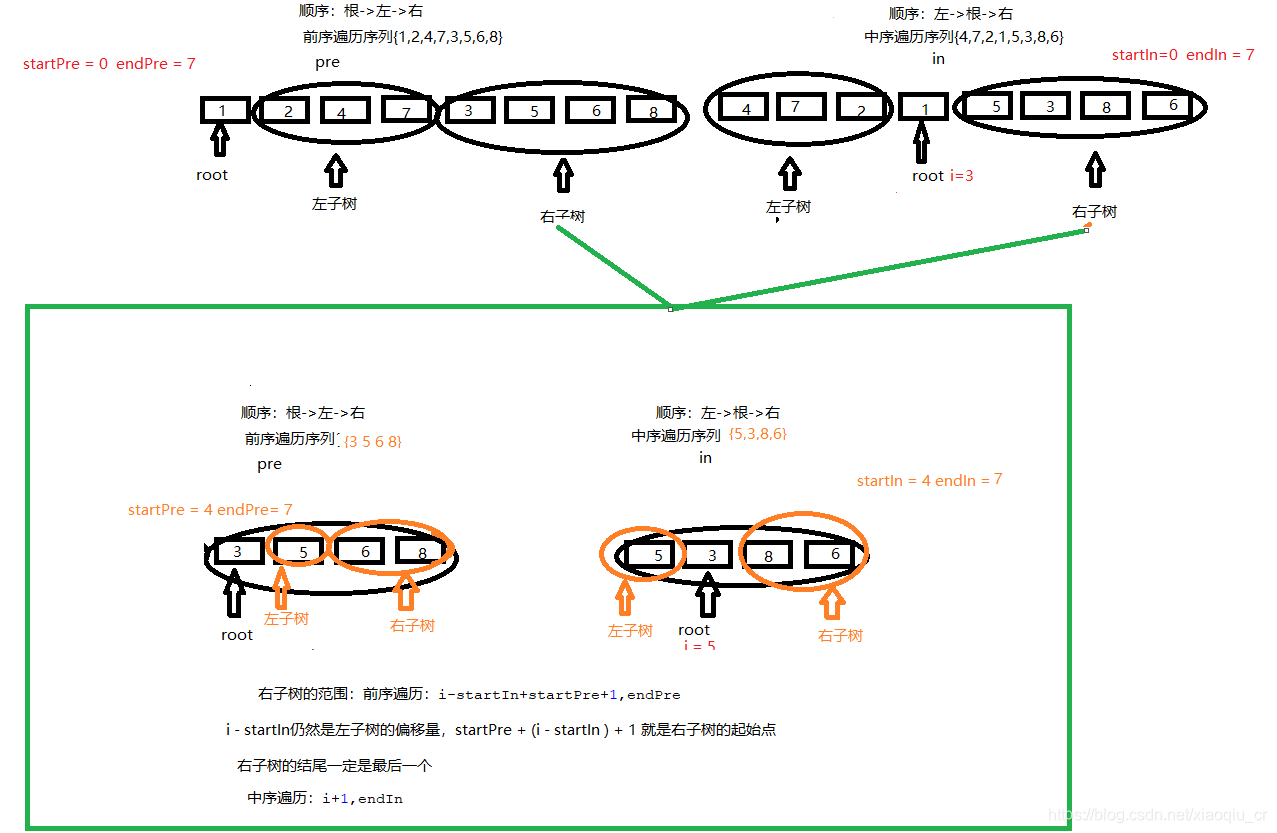
question：输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。

resolution1：

 public class TreeNode {
            int val;
            TreeNode left;
            TreeNode right;
            TreeNode(int x) { val = x; }
        }

        public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
            TreeNode root=reConstructBinaryTree(pre,0,pre.length-1,in,0,in.length-1);
            return root;
        }
        //对reConstructBinaryTree方法进行一个重载，添加前序数组和中序遍历数组的起始和结尾点
        //前序遍历{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}
        private TreeNode reConstructBinaryTree(int [] pre,int startPre,int endPre,int [] in,int startIn,int endIn) {
            //设置递归的终止条件
            if(startPre>endPre||startIn>endIn)
                return null;
            //对于前序遍历来说，第一个数值肯定是根节点，所以每进入该方法，对于任何一个长度的前序数组来说，都可以将第一个节点转为根节点对象
            TreeNode root=new TreeNode(pre[startPre]);

            //对于中序数组来说，依次遍历直到找到前序数组的第一个数为止，作为左右子树的分界线
            for(int i=startIn;i<=endIn;i++)
                if(in[i]==pre[startPre]){
                    //再分别针对左右子树进行分割，这里需要找到左右子树的前序遍历和中序遍历的起点和终点
                    root.left=reConstructBinaryTree(pre,startPre+1,startPre+i-startIn,in,startIn,i-1);
                    root.right=reConstructBinaryTree(pre,i-startIn+startPre+1,endPre,in,i+1,endIn);
                    break;
                }

            return root;
        }