将SVD应用于推荐系统

1、什么是SVD

singular value decomposition 奇异值分解，通过SVD实现从噪声数据中抽取相关特征

2、SVD的应用

2.1信息检索

隐形语义索引LSI：latent semantic indexing

隐形语义分析LSA：latent semantic analysis

再LSA中，一个矩阵是由文档和词语构成，我们利用SVD对矩阵进行分解，就会得到多个奇异值，这些奇异值代表了文档的概念和主题，我们从成千上万篇文档抽取出相同的概念和主题，那么当我们进行文档搜索的时候，匹配的就不仅仅是同义词，而是相似的概念和主题，那么就极大的增加了搜索的准确度和效率

2.2推荐系统

3、SVD如何应用于推荐系统

3.1利用SVD进行矩阵分解

SVD将原始矩阵分解成3个矩阵

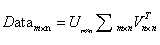
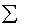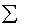这里的只有对角元素，其他值为0，且对角元素的值按照从大到小的顺序排列

他的对角元素的值是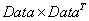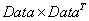特征值的平方根

from numpy import *
from numpy import linalg as la

def loadExData():
    return[[0, 0, 0, 2, 2],
           [0, 0, 0, 3, 3],
           [0, 0, 0, 1, 1],
           [1, 1, 1, 0, 0],
           [2, 2, 2, 0, 0],
           [5, 5, 5, 0, 0],
           [1, 1, 1, 0, 0]]

if __name__ == '__main__':
    data = loadExData()
    U,Sigma,VT = linalg.svd(data)
    print("U",U)
    print("Sigma",Sigma)
    print("VT",VT)

'''
U [[ -2.22044605e-16   5.34522484e-01   8.41650989e-01   5.59998398e-02
   -5.26625636e-02   2.77555756e-17   1.38777878e-17]
 [  0.00000000e+00   8.01783726e-01  -4.76944344e-01  -2.09235996e-01
    2.93065263e-01  -4.01696905e-17  -2.77555756e-17]
 [  0.00000000e+00   2.67261242e-01  -2.52468946e-01   5.15708308e-01
   -7.73870662e-01   1.54770403e-16   0.00000000e+00]
 [ -1.79605302e-01   0.00000000e+00   7.39748546e-03  -3.03901436e-01
   -2.04933639e-01   8.94308074e-01  -1.83156768e-01]
 [ -3.59210604e-01   0.00000000e+00   1.47949709e-02  -6.07802873e-01
   -4.09867278e-01  -4.47451355e-01  -3.64856984e-01]
 [ -8.98026510e-01   0.00000000e+00  -8.87698255e-03   3.64681724e-01
    2.45920367e-01  -1.07974660e-16  -1.12074131e-17]
 [ -1.79605302e-01   0.00000000e+00   7.39748546e-03  -3.03901436e-01
   -2.04933639e-01   5.94635264e-04   9.12870736e-01]]
Sigma [  9.64365076e+00   5.29150262e+00   7.40623935e-16   4.05103551e-16 2.21838243e-32]
VT [[ -5.77350269e-01  -5.77350269e-01  -5.77350269e-01   0.00000000e+00
    0.00000000e+00]
 [ -2.46566547e-16   1.23283273e-16   1.23283273e-16   7.07106781e-01
    7.07106781e-01]
 [ -7.83779232e-01   5.90050124e-01   1.93729108e-01  -2.77555756e-16
   -2.22044605e-16]
 [ -2.28816045e-01  -5.64364703e-01   7.93180748e-01   1.11022302e-16
   -1.11022302e-16]
 [  0.00000000e+00   0.00000000e+00   0.00000000e+00  -7.07106781e-01
    7.07106781e-01]]

'''

我们可以看到这里的Σ矩阵后三个数的数量级非常小，以至于可以把他们忽略，所以这里我们只取前面两个数

那么原始数据集就可以近似的等价为

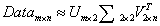
3.2重构原始矩阵

if __name__ == '__main__':
    data = loadExData()
    U,Sigma,VT = linalg.svd(data)
    Sigma = mat([[Sigma[0],0],[0,Sigma[1]]])
    u = U[:,:2]
    v = VT[:2, :]
    print(u * Sigma * v)
'''
[[  5.38896529e-16   1.58498979e-15   1.58498979e-15   2.00000000e+00
    2.00000000e+00]
 [ -1.04609326e-15   5.23046632e-16   5.23046632e-16   3.00000000e+00
 3.00000000e+00]
[ -3.48697754e-16   1.74348877e-16   1.74348877e-16   1.00000000e+00
1.00000000e+00]
[  1.00000000e+00   1.00000000e+00   1.00000000e+00   0.00000000e+00
   0.00000000e+00]
[  2.00000000e+00   2.00000000e+00   2.00000000e+00   0.00000000e+00
0.00000000e+00]
[  5.00000000e+00   5.00000000e+00   5.00000000e+00   0.00000000e+00
   0.00000000e+00]
[  1.00000000e+00   1.00000000e+00   1.00000000e+00   0.00000000e+00
0.00000000e+00]]
'''

3.3推荐未尝过的菜肴

#给定相似度计算的方法之下，用户对物品的估计评分值
def standEst(dataMat, user, simMeas, item):
    '''

    :param dataMat: 数据矩阵
    :param user:用户编号
    :param simMeas:相似度计算方法
    :param item:物品编号
    :return:
    '''
    #n表示物品数
    n = shape(dataMat)[1]
    simTotal = 0.0;
    ratSimTotal = 0.0
    #遍历所有的物品
    for j in range(n):
        #该用户对每个物品的评分
        userRating = dataMat[user,j]
        #如果没有评价过该物品
        if userRating == 0:
            continue
        #找到两个物品同时被评分的用户的编号（第一个元素表示行的维度）
        overLap = nonzero(logical_and(dataMat[:,item].A>0, dataMat[:,j].A>0))[0]
        if len(overLap) == 0:
            similarity = 0
        else:
            #通过用户的评分计算这两个物品的相似度（距离）
            similarity = simMeas(dataMat[overLap,item], dataMat[overLap,j])
        print ('the %d and %d similarity is: %f' % (item, j, similarity))
        simTotal += similarity
        #将该物品乘上计算的相似度，然后得到累加的相似度
        ratSimTotal += similarity * userRating
    if simTotal == 0:
        return 0
    else:
        return ratSimTotal/simTotal

#推荐估计评分最大的前N个
def recommend(dataMat, user, N=3, simMeas= cosSim, estMethod=standEst):
    #找出该用户没有评价过的商品的商品编号
    unratedItems = nonzero(dataMat[user,:].A==0)[1]#find unrated items
    if len(unratedItems) == 0:
        return 'you rated everything'
    itemScores = []
    for item in unratedItems:
        #对没有评分的商品进行估计评分
        estimatedScore = estMethod(dataMat, user, simMeas, item)
        itemScores.append((item, estimatedScore))
    #选出前N个商品
    return sorted(itemScores, key=lambda jj: jj[1], reverse=True)[:N]

计算相关系数的方法

#欧氏距离
def ecludSim(inA,inB):
    return 1.0/(1.0 + la.norm(inA - inB))

#皮尔逊相关系数
def pearsSim(inA,inB):
    if len(inA) < 3 : return 1.0
    return 0.5+0.5*corrcoef(inA, inB, rowvar = 0)[0][1]

#余弦相似度计算
def cosSim(inA,inB):
    num = float(inA.T*inB)
    denom = la.norm(inA)*la.norm(inB)
    return 0.5+0.5*(num/denom)

测试：

对2号用户进行推荐

if __name__ == '__main__':
    data = mat(loadExData())
    result = recommend(data, 2)
    print(result)

[(2, 2.5), (1, 2.0243290220056256)]

3.4利用SVD提高推荐效果

对原始数据进行SVD分割，计算矩阵sigma的平方和总能量，取出大于总能量的90%的元素，从而达到对原始数据进行降维的效果

def loadExData2():
    return[[0, 0, 0, 0, 0, 4, 0, 0, 0, 0, 5],
           [0, 0, 0, 3, 0, 4, 0, 0, 0, 0, 3],
           [0, 0, 0, 0, 4, 0, 0, 1, 0, 4, 0],
           [3, 3, 4, 0, 0, 0, 0, 2, 2, 0, 0],
           [5, 4, 5, 0, 0, 0, 0, 5, 5, 0, 0],
           [0, 0, 0, 0, 5, 0, 1, 0, 0, 5, 0],
           [4, 3, 4, 0, 0, 0, 0, 5, 5, 0, 1],
           [0, 0, 0, 4, 0, 4, 0, 0, 0, 0, 4],
           [0, 0, 0, 2, 0, 2, 5, 0, 0, 1, 2],
           [0, 0, 0, 0, 5, 0, 0, 0, 0, 4, 0],
           [1, 0, 0, 0, 0, 0, 0, 1, 2, 0, 0]]

if __name__ == '__main__':
    data = mat(loadExData2())
    U,Sigma,VT = linalg.svd(data)
    Sigma2 = Sigma ** 2
    print(Sigma2)
    #总能量的90%
    print(sum(Sigma2) * 0.9)
    #前两个元素的总能量
    print(sum(Sigma2[:2]))
    #前三个元素的总能量
    print(sum(Sigma2[:3]))
'''
[  2.48716665e+02   1.30112895e+02   1.21670730e+02   2.34875695e+01
   9.56615756e+00   6.66142570e+00   1.00828796e+00   5.30232598e-01
   1.91847092e-01   4.87619735e-02   5.42848136e-03]
487.8
378.829559511
500.500289128
'''

于是将一个11维的原始矩阵降维为3维的原始矩阵

if __name__ == '__main__':
    data = mat(loadExData2())
    U,Sigma,VT = linalg.svd(data)
    #构建3维sigma矩阵
    Sigma = mat([[Sigma[0],0,0],[0,Sigma[1],0],[0,0,Sigma[2]]])
    #重构原始矩阵
    data = U[:,:3] * Sigma * VT[:3,:]
    print(data)

将上述过程整合如下为基于SVD的评分估计

#基于SVD的评分估计
def svdEst(dataMat, user, simMeas, item):
    #取出商品数
    n = shape(dataMat)[1]
    simTotal = 0.0;
    ratSimTotal = 0.0
    U,Sigma,VT = la.svd(dataMat)
    #对原始数据进行重构
    Sig4 = mat(eye(4)*Sigma[:4]) #arrange Sig4 into a diagonal matrix
    xformedItems = dataMat.T * U[:,:4] * Sig4.I  #create transformed items
    for j in range(n):
        userRating = dataMat[user,j]
        if userRating == 0 or j==item:
            continue
        #计算两个商品的相似度
        similarity = simMeas(xformedItems[item,:].T, xformedItems[j,:].T)
        print ('the %d and %d similarity is: %f' % (item, j, similarity))
        #计算该商品和所有商品的累加相似度
        simTotal += similarity
        #计算估计评分
        ratSimTotal += similarity * userRating
    if simTotal == 0:
        return 0
    else:
        #对估计评分进行归一化处理
        return ratSimTotal/simTotal

推荐物品及相应估计评分如下

if __name__ == '__main__':
    data = mat(loadExData2())
    result = recommend(data, 1)
    print(result)
# [(4, 3.3447149384692278), (7, 3.3294020724526971), (9, 3.328100876390069)]

4、SVD应用于图像压缩

def printMat(inMat, thresh=0.8):
    '''
    #打印矩阵：
    :param inMat: 输入矩阵32*32=1024像素的矩阵
    :param thresh: 阈值
    :return:
    '''
    for i in range(32):
        for k in range(32):
            #大于阈值打印1，否则打印0
            if float(inMat[i,k]) > thresh:
                print(1,end=' ')
            else: print(0,end=' ')
        print ('')

def imgCompress(numSV=2, thresh=0.8):
    '''
    图像压缩函数
    :param numSV:
    :param thresh:
    :return:
    '''
    myl = []
    for line in open('D:\0_5.txt').readlines():
        newRow = []
        for i in range(32):
            newRow.append(int(line[i]))
        myl.append(newRow)
    myMat = mat(myl)
    print ("****original matrix******")
    printMat(myMat, thresh)
    #对原始矩阵进行SVD分割
    U,Sigma,VT = la.svd(myMat)
    #创建一个3*3的零矩阵
    SigRecon = mat(zeros((numSV, numSV)))
    for k in range(numSV):#construct diagonal matrix from vector
        #取出sigma的前3个元素构建对角矩阵
        SigRecon[k,k] = Sigma[k]
    #重构原始矩阵
    reconMat = U[:,:numSV] * SigRecon * VT[:numSV,:]
    print ("****reconstructed matrix using %d singular values******" % numSV)
    printMat(reconMat, thresh)

if __name__ == '__main__':
    imgCompress()

****original matrix******
0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 
0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 
0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 
0 0 0 0 0 0 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 
0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 
0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 
0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 
0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 
0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 
0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 
0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 
0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 
****reconstructed matrix using 2 singular values******
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 

我们可以看到经过压缩后的图像几乎和原来的数字一摸一样，由于压缩后的矩阵U为32 * 2 ,VT矩阵为2 * 32 ，sigma的个数为2 所以压缩后的总的像素为64 + 64 + 2 = 130

那么我们可以得到压缩比为1024/130=7.876923076923077

所以采用SVD进行图像压缩可以有效的减少空间和带宽开销