PCA主成分分析进行数据降维

1、PCA的原理

PCA:principal component analysis 主成分分析，PCA通过更换数据的坐标系来达到降维的目的。

第一个坐标轴是原始数据的方差最大的方向，第二个坐标轴是与第一个坐标轴正交并且方差次大的方向

2、PCA的优缺点

优点：降低数据的复杂性，识别最重要的多个特征

缺点：不一定需要，且有可能损失重要信息

3、PCA伪代码

'''
去除平均值
计算协方差矩阵
计算协方差矩阵的特征值和特征向量
将特征值从大到小排序
保留最上面的#个特征向量
将数据转换到上述#个特征向量构建的新空间中
'''

4、代码准备

from numpy import *
import numpy as np
import matplotlib
import matplotlib.pyplot as plt

def loadDataSet(fileName, delim='	'):
    fr = open(fileName)
    data = []
    for line in fr.readlines():
       dataLine = list(map(float, line.strip().split(delim)))
       data.append(dataLine)
    return mat(data)

def pca(dataMat, topNfeat=9999999):
    '''
    :param dataMat: 原始数据集
    :param topNfeat: 应用的特征
    :return:
    '''
    meanVals = mean(dataMat, axis=0)
    '''
    axis 不设置值，对 m*n 个数求均值，返回一个实数

    axis = 0：压缩行，对各列求均值，返回 1* n 矩阵
    
    axis =1 ：压缩列，对各行求均值，返回 m *1 矩阵  
    '''
    meanRemoved = dataMat - meanVals #remove mean
    #计算协方差矩阵
    covMat = cov(meanRemoved, rowvar=0)
    #计算特征值和特征向量
    eigVals,eigVects = linalg.eig(mat(covMat))
    #将特征值按照从小到大的顺序排列，提取出索引值
    eigValInd = argsort(eigVals)            #sort, sort goes smallest to largest
    #从末尾最大的元素开始，步长为-1，一直到-(topNfeat+1)（左闭右开）
    #反转,截取部分索引值
    eigValInd = eigValInd[:-(topNfeat+1):-1]  #cut off unwanted dimensions
    #取出对应特征值对应的特征向量
    #选出topFeat个最大特征向量
    redEigVects = eigVects[:,eigValInd]       #reorganize eig vects largest to smallest
    #将数据转换到低维新空间
    lowDDataMat = meanRemoved * redEigVects#transform data into new dimensions
    reconMat = (lowDDataMat * redEigVects.T) + meanVals
    return lowDDataMat, reconMat

if __name__ == '__main__':
    data_set = loadDataSet("D://pca//testSet.txt",delim='	')
    lowDDataMat, reconMat = pca(data_set,1)
    n = shape(lowDDataMat)
    print(n)
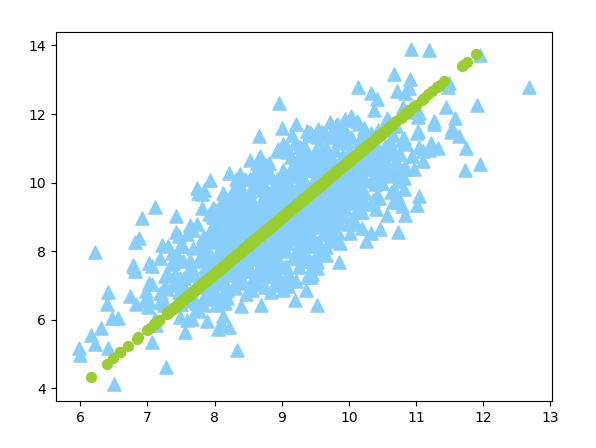
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(data_set[:,0].flatten().A[0],data_set[:,1].flatten().A[0],marker='^',s = 90,c='lightskyblue')
    ax.scatter(reconMat[:,0].flatten().A[0],reconMat[:,1].flatten().A[0],marker='o',s = 50,c='yellowgreen')
    plt.show()

(1000, 1)