Bspline CatmullRoom and Bezier 样条曲线生成

此项目旨在生成常见的样条曲线，项目inspired by 叶飞影

样条曲线：转述知乎答案解释其意义。

预备知识：已知离散的数据，但不知函数表达式，插值和拟合都是为了寻找函数表达式。区别在于，插值得到的函数能够穿过已知的点（在已知的点的函数表达式的值等于已知数值，但容易出现龙格现象），拟合只求函数图形神似而不求穿过已知点。

那么怎么能既穿过已知点又能让函数图形像呢？就是怎么避免龙格现象呢？

答案是分段插值，就是将全部数据分割成若干部分，每个小部分用插值得到不同的函数，最后用很多不同的函数表达原来的序列。问题又来了，不同函数两端衔接不好怎么办？

答案是高次样条差值，既每个分段函数都采用高次函数形式来构造（三次样条差值 就是用x的三次方形式构造）这就保证了得到的多个函数关系式在先接触具有n-1次的连续可导性质（翻译成人话就是衔接保证光滑）

一句话总结：三次样条插值就是将原始长序列分割成若干段构造多个三次函数（每段一个），使得分段的衔接处具有二阶导数连续的性质（也就是光滑衔接）。

其中“三次”只函数基本形式使用三次函数的形式。“样条”是一种手艺，指加工曲面时使得曲面光滑的手艺。“插值”你肯定知道是啥意思了~~

此处答案虽然针对三次样条插值，但是可以很好解释样条插值的概念。

首先是各种曲线的基类

#ifndef __SPLINE_BASE__
#define __SPLINE_BASE__

#include <cstddef>

class SplineBase
{
public:
    // 计算样条数值
    virtual bool BuildSpline(const void* ctrlValuesPtr, int ctrlStride, int ctrlCount, void* splineValuesPtr, int splineStride) const = NULL;

    // 计算切线数值
    virtual bool BuildTangent(const void* ctrlValuesPtr, int ctrlStride, int ctrlCount, void* tangentValuesPtr, int tangentStride) const
    {
        return false;
    }
};

inline float YfGetFloatValue(const void* valuesPtr, int stride, int index)
{
    return *(float*)((char*)valuesPtr + stride * index);
}

#endif //__SPLINE_BASE__

每种曲线的类都会继承此基类，并实现 BuildSpline或者同时实现BuildSpline和Buildtangent两个函数。三种曲线中，三阶及以上阶数的Bezier曲线只通过起始控制点和终点，B样条曲线不会经过其控制点，CatmullRoom曲线会通过所有控制点。BSpline和CatmullRoom样条公式要求4个控制点，然后给出位于第2和第3点之间的光滑曲线(效果如下图，图片来源游戏编程精粹1)。为了得到第1个控制点和第2个控制点之间的点，可以将第一个控制点输入两次，同理第3和第4个控制点之间的曲线需要第四点输入两次。

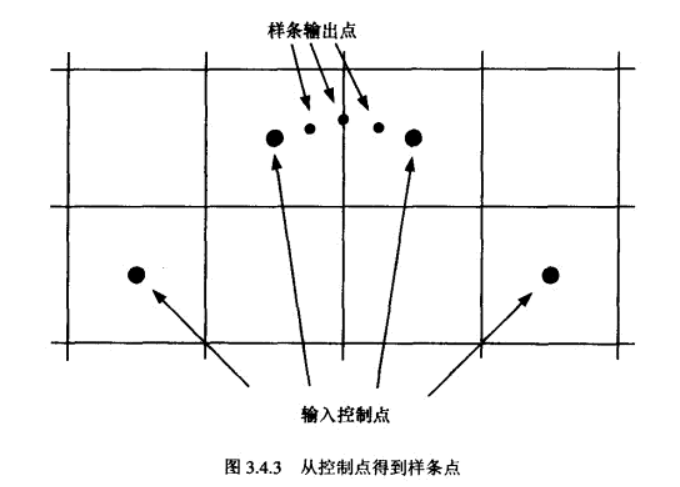
N阶Bezier 曲线

1. 原理参考我的另外一篇博客：N 阶贝塞尔曲线生成，此篇代码每次都要计算N次方，比较耗时，可以在绘制图形之前，先计算好各阶数值即可。如下代码分别是bezier.h 和 bezier.cpp实现N阶贝塞尔曲线

/****************************************************************

  File name   :  bezier.h
  Author      :  Shike
  Version     :  1.0
  Create Date :  2020/05/01
  Description :  Bezier Spline

*****************************************************************/

#ifndef __BEZIER__SPLINE__
#define __BEZIER__SPLINE__

#include "spline_base.h"

#define YD_MAX_BEZIER_CONTROL_VALUE 33

class Bezier : public SplineBase
{
public:
    Bezier();
    ~Bezier();

    // 设置输出样条值的数目
    void SetSplineValuesCount(int count);

    // 获得输出样条值的数目
    int GetSplineValuesCount() const;

    // 计算样条数值
    bool BuildSpline(const void* ctrlValuesPtr, int ctrlStride, int ctrlCount, void* splineValuesPtr, int splineStride) const;

protected:
    void ClearPowT();
    void BuildPowT();
    
    double GetValueT(int t, int p) const
    {
        return m_pow_t[YD_MAX_BEZIER_CONTROL_VALUE*t + p];
    }

protected:
    int    m_valuesCount;
    double *m_pow_t;

protected:
    static void BuildYanghuiTriangle();

    //pascal's triangle
    static int  m_yanghuiRowIndex[YD_MAX_BEZIER_CONTROL_VALUE];
    static int  m_yanghuiTriangle[(YD_MAX_BEZIER_CONTROL_VALUE + 1)*YD_MAX_BEZIER_CONTROL_VALUE / 2];

};

#endif // __BEZIER__SPLINE__

bezier.cpp

#include "bezier.h"
#include "assert.h"
#include "stdlib.h"

#include <cstdio>

int Bezier::m_yanghuiRowIndex[YD_MAX_BEZIER_CONTROL_VALUE] = { 0 };
int Bezier::m_yanghuiTriangle[(YD_MAX_BEZIER_CONTROL_VALUE + 1)*YD_MAX_BEZIER_CONTROL_VALUE / 2] = { 0 };

Bezier::Bezier()
{
    if (m_yanghuiTriangle[0] == 0)
    {
        BuildYanghuiTriangle();
    }

    m_valuesCount = 0;
    m_pow_t = NULL;

    SetSplineValuesCount(100);
}

Bezier::~Bezier()
{
    ClearPowT();
}

void Bezier::BuildYanghuiTriangle()
{
    // 第0行
    m_yanghuiRowIndex[0] = 0;
    m_yanghuiTriangle[0] = 1;

    int index = 1;
    int t0, t1;
    int* lastRow;

    for (int i = 1; i < YD_MAX_BEZIER_CONTROL_VALUE; i++)
    {
        m_yanghuiRowIndex[i] = index;
        m_yanghuiTriangle[index] = 1;
        index++;

        for (int j = 1; j <= i; j++)
        {
            lastRow = m_yanghuiTriangle + m_yanghuiRowIndex[i - 1];
            t0 = lastRow[j - 1];
            t1 = (j < i) ? lastRow[j] : 0;

            m_yanghuiTriangle[index] = t0 + t1;
            index++;
        }
    }

    assert(index == (YD_MAX_BEZIER_CONTROL_VALUE + 1)*YD_MAX_BEZIER_CONTROL_VALUE / 2);
}

//设置输出样条值的数目
void Bezier::SetSplineValuesCount(int count)
{
    if (count < 2)
    {
        count = 2;
    }

    if (count == m_valuesCount)
    {
        return;
    }

    m_valuesCount = count;
    BuildPowT();
}

//获得输出样条值的数目
int Bezier::GetSplineValuesCount() const
{
    return m_valuesCount;
}

void Bezier::ClearPowT()
{
    if (m_pow_t)
    {
        free(m_pow_t);
        m_pow_t = NULL;
    }
}

void Bezier::BuildPowT()
{
    ClearPowT();

    m_pow_t = (double*)malloc(m_valuesCount*YD_MAX_BEZIER_CONTROL_VALUE * sizeof(double));
    double t;
    for (int i = 0; i < m_valuesCount; i++)
    {
        t = i / (m_valuesCount - 1.0f);

        m_pow_t[i*YD_MAX_BEZIER_CONTROL_VALUE] = 1.0f;
        for (int j = 1; j < YD_MAX_BEZIER_CONTROL_VALUE; j++)
        {
            m_pow_t[i*YD_MAX_BEZIER_CONTROL_VALUE + j] = m_pow_t[i*YD_MAX_BEZIER_CONTROL_VALUE + j - 1] * t;
        }
    }
}

//计算样条数值
bool Bezier::BuildSpline(const void* ctrlValuesPtr, int ctrlStride, int ctrlCount, void* splineValuesPtr, int splineStride) const
{
    if (ctrlCount < 2 || ctrlCount > YD_MAX_BEZIER_CONTROL_VALUE)
    {
        return false;
    }

    double* destValue;
    double* srcValue;
    double v;
    const int* yanghuiRow = m_yanghuiTriangle + m_yanghuiRowIndex[ctrlCount - 1];

    for (int i = 0; i < m_valuesCount; i++)
    {
        for (int dim = 0; dim < ctrlStride; dim++)
        {
            v = 0.0f;
            for (int j = 0; j < ctrlCount; j++)
            {
                srcValue = (double*)ctrlValuesPtr + ctrlStride * j + dim;
                v += yanghuiRow[j] * (*srcValue) * GetValueT(i, j) * GetValueT(m_valuesCount - 1 - i, ctrlCount - 1 - j);
            }

            destValue = (double*)splineValuesPtr + splineStride * i + dim;
            *destValue = v;
        }
    }

    return true;
}

显示效果如下

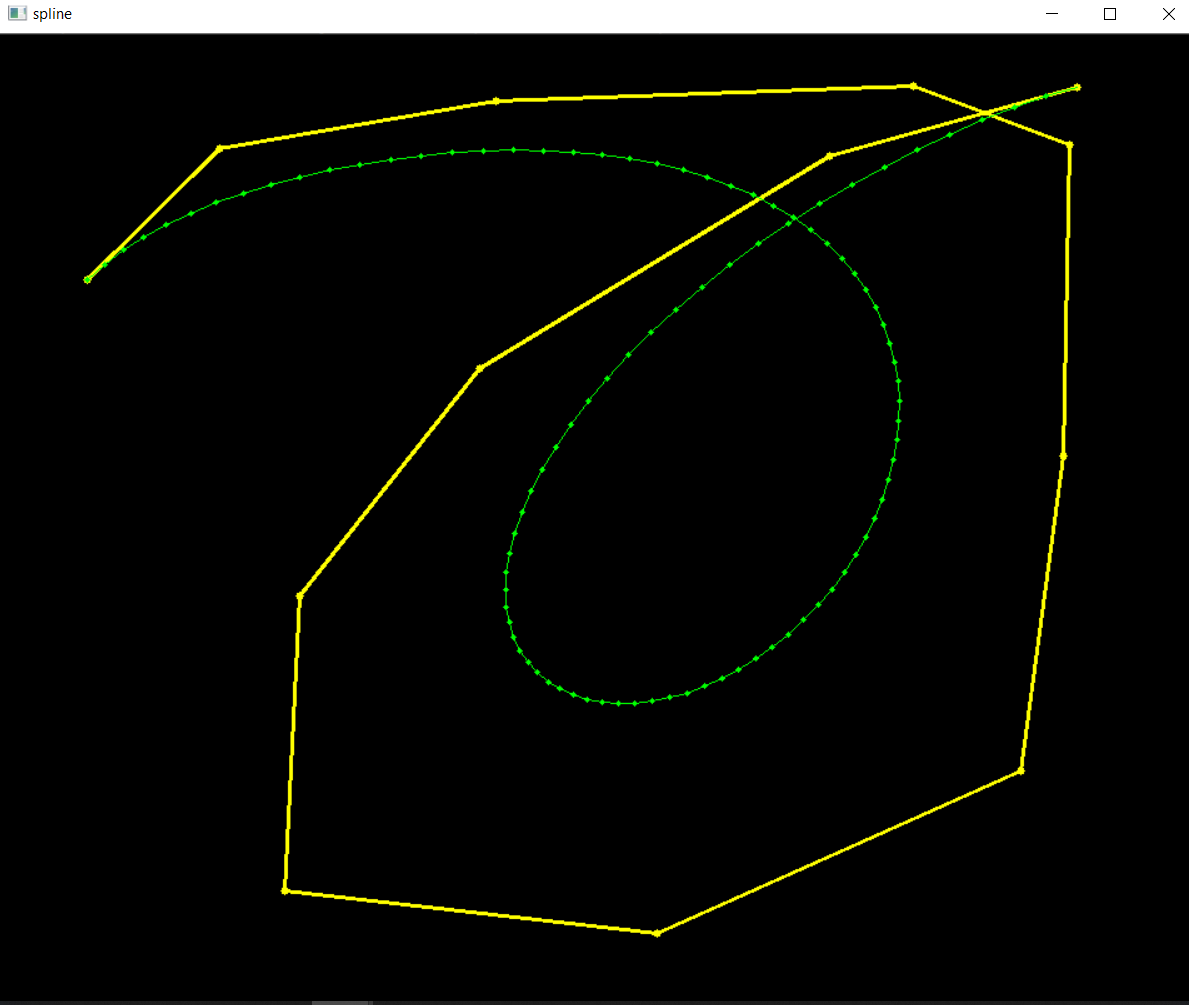
BSpline 

在数学的子学科数值分析里，B-样条是样条曲线一种特殊的表示形式。它是B-样条基曲线的线性组合。B-样条是贝兹（贝塞尔）曲线的一种一般化，可以进一步推广为非均匀有理B样条(NURBS)，使得我们能给更多一般的几何体建造精确的模型。

常数B样条

常数B样条是最简单的样条。只定义在一个节点距离上，而且不是节点的函数。它只是不同节点段（knot span）的标志函数（indicator function）。

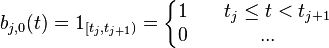
线性B样条

线性B样条定义在两个相邻的节点段上，在节点连续但不可微。

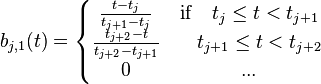
三次B样条

一个片断上的B样条的表达式可以写作：

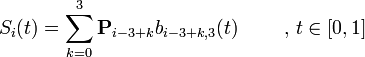
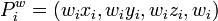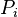 其中S_i是第i个B样条片段，而P是一个控制点集，i和k是局部控制点索引。控制点的集合会是的集合，其中是比重，当它增加时曲线会被拉向控制点，在减小时则把曲线远离该点。片段的整个集合m-2条曲线（）由m+1个控制点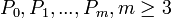（）定义，作为t上的一个B样条可以定义为

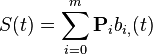
其中i是控制点数，t是取节点值的全局参数。这个表达式把B样条表示为B样条基函数的线性组合，这也是这个名称的原因。有两类B样条-均匀和非均匀。非均匀B样条相邻控制点间的距离不一定要相等。一个一般的形式是区间随着插入控制点逐步变小到0。

bspline.cpp核心代码

void BSpline::BuildWeights()
{
    ClearWeights();

    m_splineWeights = (double **)malloc(4 * sizeof(double*));
    m_tangentWeights = (double **)malloc(4 * sizeof(double*));

    for (int i = 0; i < 4; i++)
    {
        m_splineWeights[i] = (double*)malloc((m_subD) * sizeof(double));
        m_tangentWeights[i] = (double*)malloc((m_subD) * sizeof(double));
    }

    double u, u_2, u_3;
    for (int i = 0; i < m_subD; i++)
    {
        u = (float)i / m_subD;
        u_2 = u * u;
        u_3 = u_2 * u;

        // 参见"游戏编程精粹1"P331
        m_splineWeights[0][i] = (-1.0f*u_3 + 3.0f*u_2 - 3.0f*u + 1.0f) / 6.0f;
        m_splineWeights[1][i] = (3.0f*u_3 - 6.0f*u_2 + 0.0f*u + 4.0f) / 6.0f;
        m_splineWeights[2][i] = (-3.0f*u_3 + 3.0f*u_2 + 3.0f*u + 1.0f) / 6.0f;
        m_splineWeights[3][i] = (1.0f*u_3 + 0.0f*u_2 + 0.0f*u + 0.0f) / 6.0f;

        // 参见"游戏编程精粹1"P333
        m_tangentWeights[0][i] = (-1.0f*u_2 + 2.0f*u - 1.0f)*0.5f;
        m_tangentWeights[1][i] = (3.0f*u_2 - 4.0f*u + 0.0f)*0.5f;
        m_tangentWeights[2][i] = (-3.0f*u_2 + 2.0f*u + 1.0f)*0.5f;
        m_tangentWeights[3][i] = (1.0f*u_2 + 0.0f*u + 0.0f)*0.5f;
    }
}

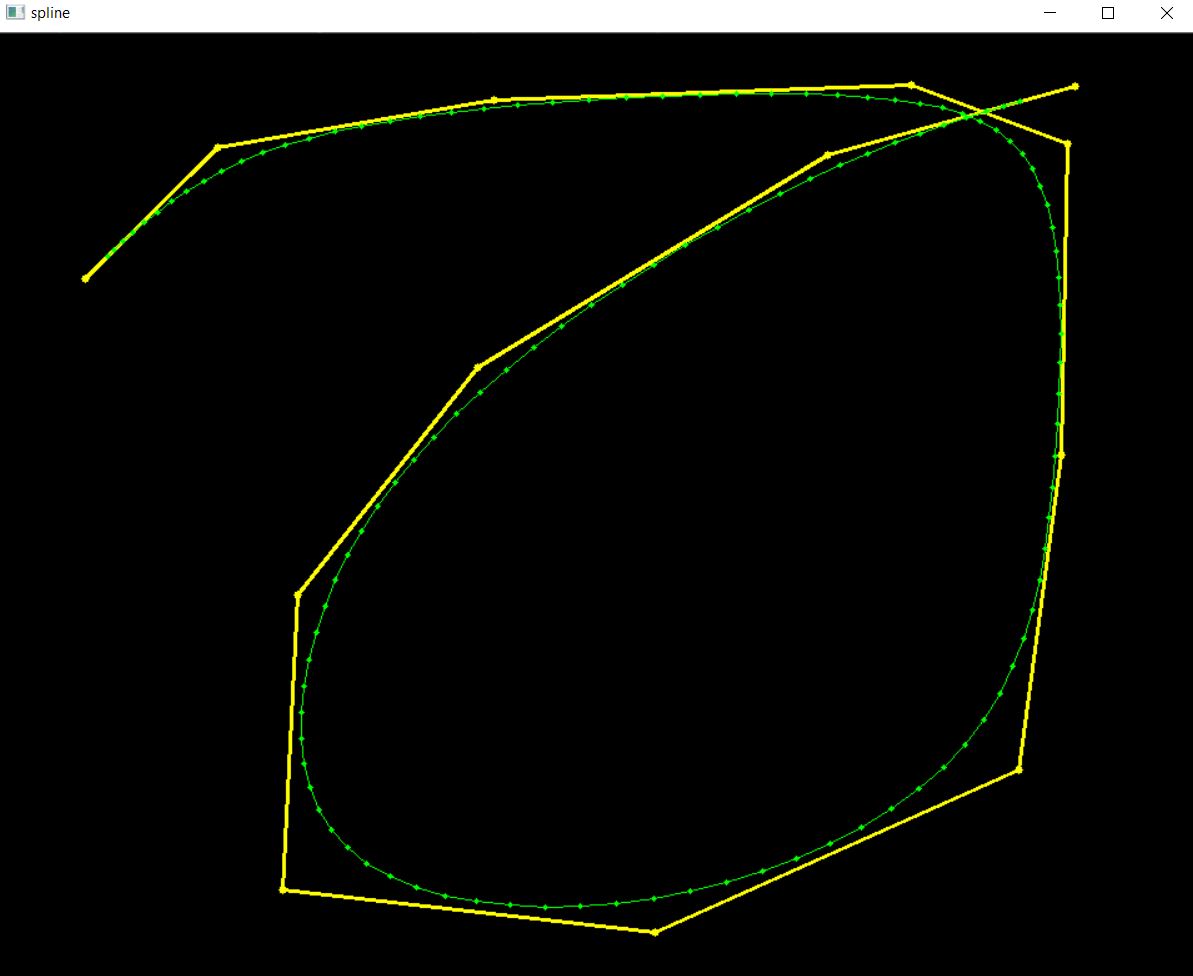
显示效果如下

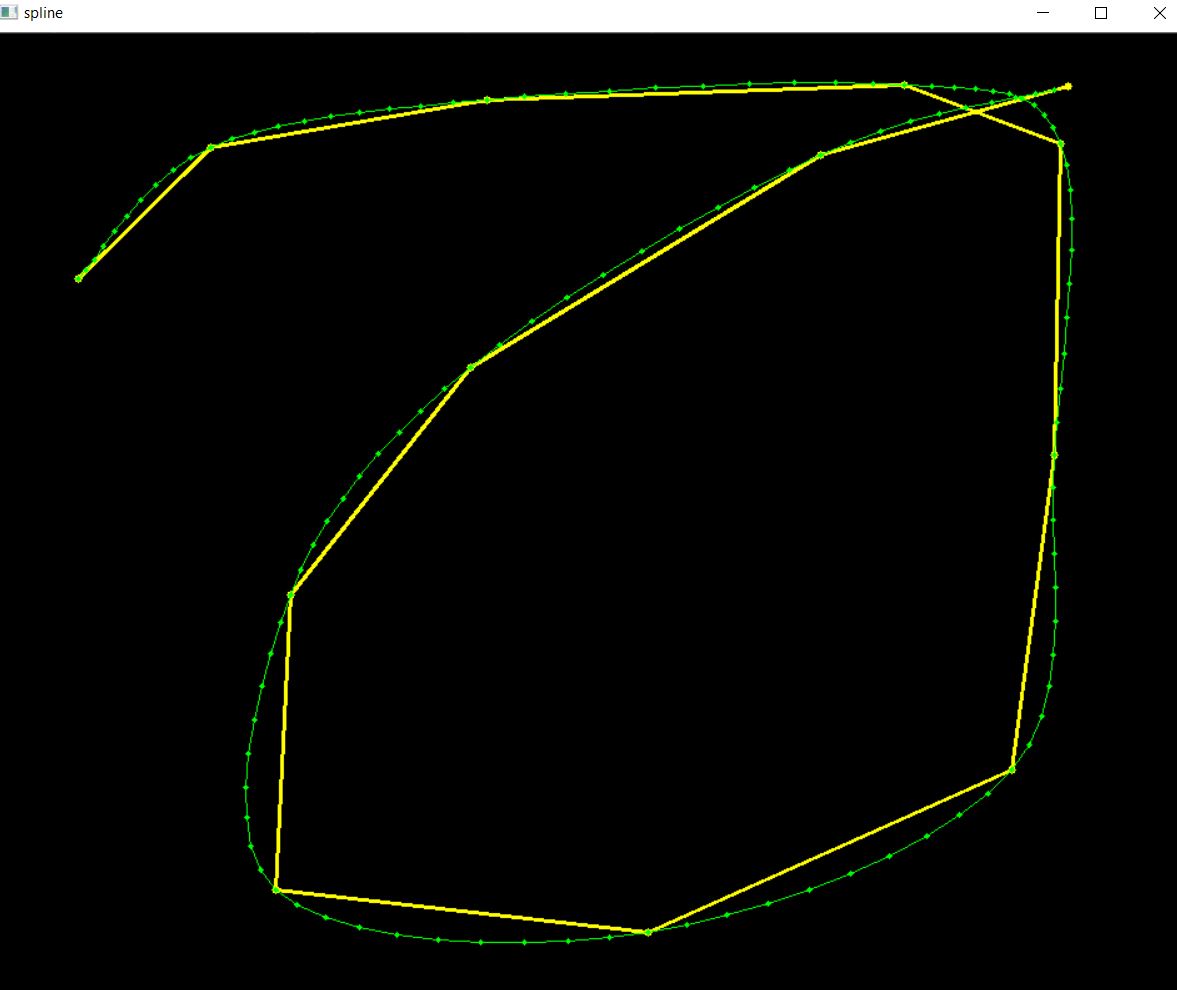
CatmullRoom

所谓样条曲线是指给定一组控制点而得到一条曲线，曲线的大致形状由这些点予以控制，一般可分为插值样条和逼近样条两种，插值样条通常用于数字化绘图或动画的设计，逼近样条一般用来构造物体的表面。CatmullRom样条与上一节所讲的B样条很相似，不同在于CatmullRom样条的曲线会经过其每一个控制点。

catmullroom.cpp核心代码入下

void CatmullRoom::BuildWeights()
{
    ClearWeights();

    m_splineWeights = (double **)malloc(4 * sizeof(double*));
    m_tangentWeights = (double **)malloc(4 * sizeof(double*));

    for (int i = 0; i < 4; i++)
    {
        m_splineWeights[i] = (double*)malloc((m_subD) * sizeof(double));
        m_tangentWeights[i] = (double*)malloc((m_subD) * sizeof(double));
    }

    double u, u_2, u_3;
    for (int i = 0; i < m_subD; i++)
    {
        u = (float)i / m_subD;
        u_2 = u * u;
        u_3 = u_2 * u;

        // 参见"游戏编程精粹1"P333
        m_splineWeights[0][i] = (-1.0f*u_3 + 2.0f*u_2 - 1.0f*u + 0.0f)*0.5f;
        m_splineWeights[1][i] = (3.0f*u_3 - 5.0f*u_2 + 0.0f*u + 2.0f)*0.5f;
        m_splineWeights[2][i] = (-3.0f*u_3 + 4.0f*u_2 + 1.0f*u + 0.0f)*0.5f;
        m_splineWeights[3][i] = (1.0f*u_3 - 1.0f*u_2 + 0.0f*u + 0.0f)*0.5f;

        m_tangentWeights[0][i] = (-3.0f*u_2 + 4.0f*u - 1.0f)*0.5f;
        m_tangentWeights[1][i] = (9.0f*u_2 - 10.0f*u + 0.0f)*0.5f;
        m_tangentWeights[2][i] = (-9.0f*u_2 + 8.0f*u + 1.0f)*0.5f;
        m_tangentWeights[3][i] = (3.0f*u_2 - 2.0f*u + 0.0f)*0.5f;
    }
}

 博主叶飞影博客附带可样条视化工具，可以下载设置控制点检测曲线效果。此博客对应的代码地址 multiple_splines, 代码针对二维数据进行了测试，三维理论上是支持的，可能需要修改一些东西，如果有需求，可在此代码基础上进行修改