博客转载自:http://www.cnblogs.com/21207-iHome/p/5234762.html
无迹卡尔曼滤波(unscented kalman filter)中需要用到无迹变换。维基百科中对unscented transform的描述如下:
The unscented transform (UT) is a mathematical function used to estimate the result of applying a given nonlinear transformation to a probability distribution that is characterized only in terms of a finite set of statistics. The most common use of the unscented transform is in the nonlinear projection of mean and covariance estimates in the context of nonlinear extensions of the Kalman filter.
为了理解unsecnted transform首先考虑一个问题:X为服从正态分布的一维随机变量,Y是随机变量X的函数分布,那么随机变量Y的期望和方差是多少呢?
X ∼ N(µ, σ^2 ) , Y = sin(X)
根据数理统计中的理论,设连续随机变量X的概率密度为f(x),则随机变量Y=g(X)的数学期望定义为:

为此需要计算反常积分。也可以先求出Y的分布函数,求导计算概率密度,然后再根据数学期望定义计算Y的数学期望。
方差计算公式如下,可以看出要求方差需要先算出期望。
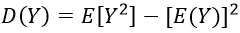
有时候反常积分比较难算或者不收敛,那么求解该问题就变得困难。下面考虑将函数y=sin(x)在x=µ处进行一阶泰勒展开,忽略高阶项,则有:
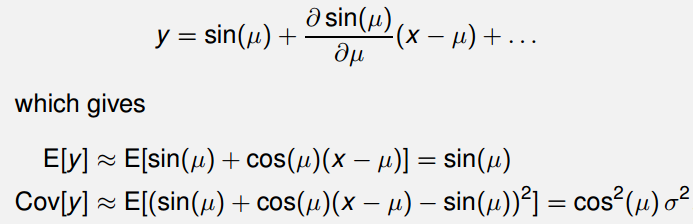
那么这个近似计算的效果怎么样呢?可以比较一下:
from numpy import sin,cos,exp,inf,pi import scipy.integrate as integrate mu = 1 # 期望 sigma = 1 # 标准差 # Y = sin(X) # 按公式计算E[Y]和D[Y] f1 = lambda x: sin(x) * exp(-(x-mu)**2/(2*sigma**2)) / ((2*pi)**0.5*sigma) f2 = lambda x: sin(x)**2 * exp(-(x-mu)**2/(2*sigma**2)) / ((2*pi)**0.5*sigma) f_mu, err = integrate.quad( f1, -inf, inf) temp, err = integrate.quad( f2, -inf, inf) f_cov = temp - f_mu**2 print f_mu, f_cov # 按一阶泰勒展开近似计算 print sin(mu), cos(mu)**2 * sigma**2
期望和方差的计算结果如下:
0.510377951545 0.267674021573
0.841470984808 0.291926581726
第一行为根据公式进行数值积分运算得到的结果,第二行为通过一阶泰勒展开近似计算得到的结果,可以看出与理论计算值相比存在一定误差。一阶泰勒展开实际上是在局部用一个线性函数去逼近非线性函数,由此可以联想到,当该处的函数呈高度非线性时按照一阶泰勒展开计算的结果会存在较大的误差。下图在某种程度上可以说明这个问题:对函数f(x)=sinx和g(x)=sin2x来说,在µ=pi/4处曲线g(x)明显比f(x)的非线性程度要大,因此同样在x=pi/4处进行一阶泰勒展开计算随机变量Y=sin(X)和Y=sin(2X)的期望,期望误差的绝对值 g(x)比f(x)要大。
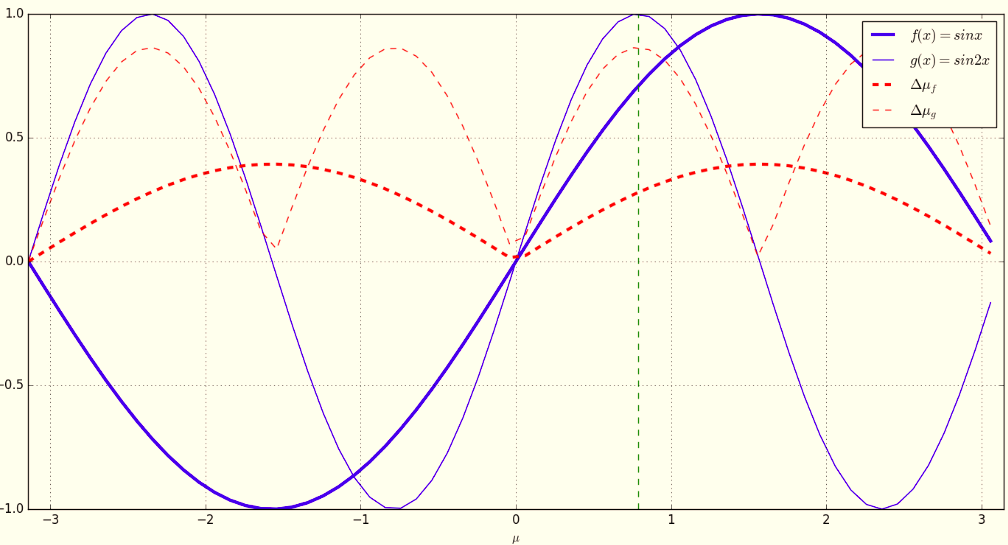
可以看出对非线性问题采用一阶泰勒展开存在着一些问题,比如:当高阶项无法忽略时会产生较大误差;函数求导困难;计算结果的精度与函数非线性程度相关等。对于这样的问题有没有其它解决办法呢?(既不用进行泰勒展开,还能保证计算精度). 联想到扩展卡尔曼滤波(Extended Kamlan Filter)也是采用类似的方法,求取雅可比矩阵,对非线性问题进行近似,因此EKF方法也存在一定缺陷,后面将逐步引出无迹卡尔曼滤波(UKF)法,并于EKF法进行对比。
参考: