动态规划（二）——升级版0-1背包问题

1 题目描述

  对于一组不同重量、不可分割的物品，我们需要选择一些装入背包，在满足背包最大重量限制的前提下，背包中物品总重量的最大值是多少呢？

  刚刚讲的背包问题，只涉及背包重量和物品重量。我们现在引入物品价值这一变量。对于一组不同重量、不同价值、不可分割的物品，我们选择将某些物品装入背包，在满足背包最大重量限制的前提下，背包中可装入物品的总价值最大是多少呢？

2 输入

  第一行是物品的个数n（1≤n≤100000），背包容量w（1≤w≤1000000）；
  第二行是n个物品的重量。

  第三行是n个物品的价值。

3 输出

  输出最大值

4 样例输入

5 9
2 2 4 6 3
3 4 8 9 6

5 样例输出

18

6 求解思路

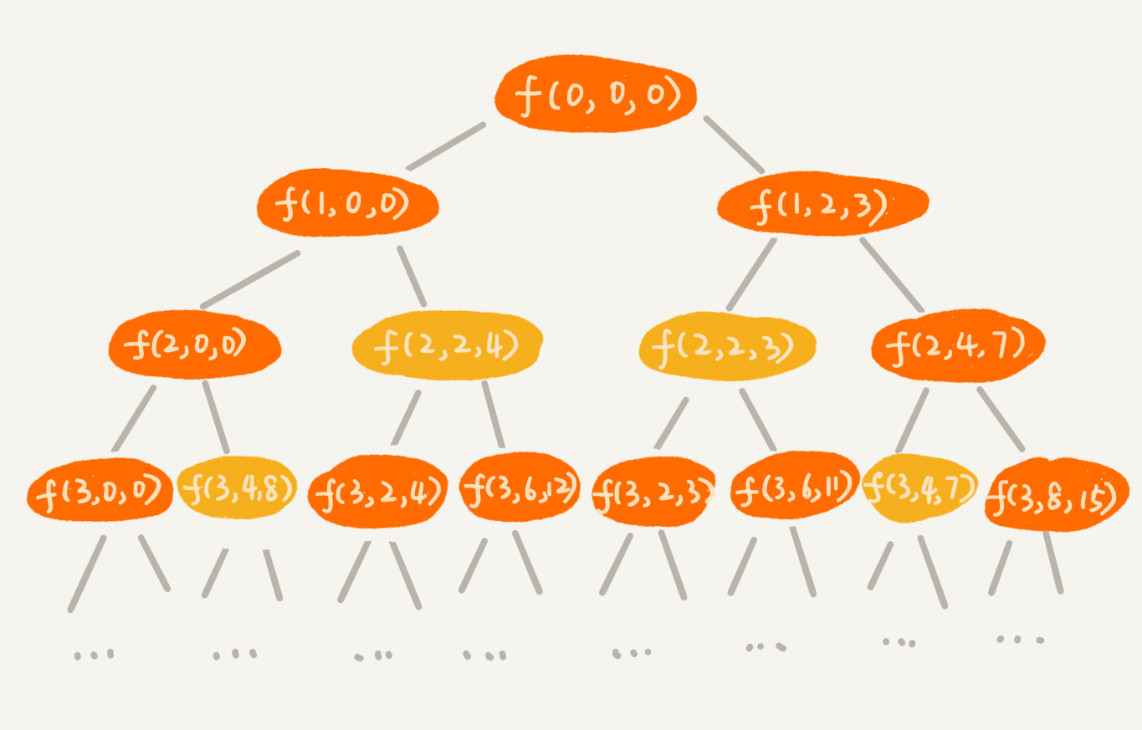
  我们发现，在递归树中，有几个节点的 i 和 cw 是完全相同的，比如 f(2,2,4) 和 f(2,2,3)。在背包中物品总重量一样的情况下，f(2,2,4) 这种状态对应的物品总价值更大，我们可以舍弃 f(2,2,3) 这种状态，只需要沿着 f(2,2,4) 这条决策路线继续往下决策就可以。
  也就是说，对于 (i, cw) 相同的不同状态，那我们只需要保留 cv 值最大的那个，继续递归处理，其他状态不予考虑。
  用一个二维数组states[n][w+1]，来记录每层可以达到的不同状态。不过这里数组存储的值不再是 bool 类型的了，而是当前状态对应的最大总价值。我们把每一层中 (i, cw) 重复的状态（节点）合并，只记录 cv 值最大的那个状态，然后基于这些状态来推导下一层的状态。
  同样的，使用回溯法与动态规划两种方法解决。

7 回溯法C++版本代码如下

#include <iostream>
#include <math.h>
#include <string.h>
using namespace std;

#define MAXNUM 100010

int maxWeight = -9999;


// 背包升级问题回溯法解决（加入背包的价值）
void secPackage(int weight[], int value[], int curV, int curW, int weightLimit, int curS, int n){
    // 如果背包总重量等于背包限制
    if(curW == weightLimit || curS == n){
        if(curV > maxWeight)
            maxWeight = curV;
        return ;
    }

    // 不装
    secPackage(weight, value, curV, curW, weightLimit, curS + 1, n);
    if(curW + weight[curS] <= weightLimit)
        // 装
        secPackage(weight, value, curV + value[curS], curW + weight[curS], weightLimit, curS + 1, n);
}

int main()
{
    int weight[5] = {2, 2, 4, 6, 3};
    int value[5] = {3, 4, 8 ,9, 6};
    // 测试回溯法
    secPackage(weight, value, 0, 0, 9, 0, 5);
    cout<<maxWeight<<endl;
    return 0;
}

8 动态规划C++版本代码如下

  其中：

states[j + weight[i]] = max(states[j + weight[i]], states[j] + value[i]);

  这行代码的意思是，背包装入重量为j + weight[i]的物品时，价值最大。

#include <iostream>
#include <math.h>
#include <string.h>
using namespace std;

#define MAXNUM 100010

int maxWeight = -9999;

// 二维数组解决，复杂度稍高，更好理解
int dpSecondPlus(int weight[], int value[], int n, int w) {
    int states[n][w + 1];
    memset(states, -1, sizeof(states));

    states[0][0] = 0;
    if (weight[0] <= w)
        states[0][weight[0]] = value[0];
    for (int i = 1; i < n; ++i) {
        for (int j = 0; j <= w; ++j)
            // 不选择第i个物品
            if (states[i - 1][j] >= 0)
                states[i][j] = states[i - 1][j];
        for (int j = 0; j <= w - weight[i]; ++j)
            // 选择第i个物品
            if (states[i-1][j] >= 0)
                states[i][j + weight[i]] = max(states[i][j + weight[i]], states[i - 1][j] + value[i]);
    }
    // 找出最大值
    int maxvalue = -999;
    for (int j = 0; j <= w; ++j) {
        if (states[n - 1][j] > maxvalue) maxvalue = states[n - 1][j];
    }
    return maxvalue;
}

// 一位数组解决，复杂度降低，标准解法
int dpSecondPPlus(int weight[], int value[], int n, int weightLimit){
    int states[weightLimit + 1];
    memset(states, -1, sizeof(states));
    // 初始化第一行数据
    states[0] = 0;
    if(weight[0] <= weightLimit)
        states[weight[0]] = value[0];
    for(int i = 1; i < n; i++){
        for(int j = 0; j <= weightLimit - weight[i]; j++){
            if(states[j] >= 0){
                states[j + weight[i]] = max(states[j + weight[i]], states[j] + value[i]);
            }
        }
    }
    int max = -1;
    for(int i = 0; i <= weightLimit; i++)
        if(states[i] > max)
            max = states[i];
    return max;
}

int main()
{
    int weight[5] = {2, 2, 4, 6, 3};
    int value[5] = {3, 4, 8 ,9, 6};
    // 测试动态规划
    cout<<dpSecondPlus(weight, value, 5, 9);
    return 0;
}