初识动态规划

  斐波那契数列的例子严格来说不算动态规划，以上旨在演示算法设计螺旋上升的过程。当问题中要求求一个最优解或在代码中看到循环和 max、min 等函数时，十有八九，需要动态规划大显身手。

  动态规划遵循一套固定的流程：递归的暴力解法 -> 带备忘录的递归解法（剪支） -> 非递归的动态规划解法。这个过程是层层递进的解决问题的过程，你如果没有前面的铺垫，直接看最终的非递归动态规划解法，当然会觉得牛逼而不可及了。

• 重叠子问题

• 无后效性

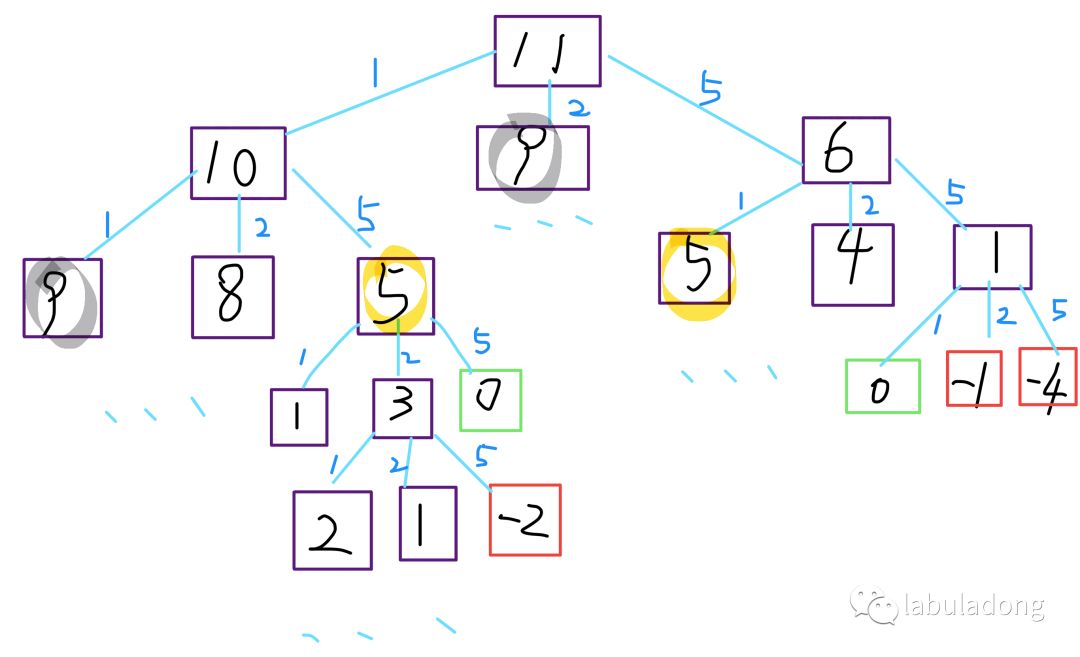
• 最优子结构：原问题的解由子问题的最优解构成。即 f(11) 由 f(10), f(9), f(6) 的最优解转移而来。要符合最优子结构，子问题间必须相互独立。

题目：给你 k 种面值的硬币，面值分别为 c1, c2 ... ck，再给一个总金额 n，问你最少需要几枚硬币凑出这个金额，如果不可能凑出，则回答 -1 。
比如说，k = 3，面值分别为 1，2，5，总金额 n = 11，那么最少需要 3 枚硬币，即 11 = 5 + 5 + 1 。下面走流程。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <vector>
//#include "MyUtils.h"
using namespace std;


// 暴力递归法
int coinChange(vector<int> &coins, int amount){

    if(amount == 0)
        return 0;
    int ans = INT_MAX;
    for(int coin : coins){
        // 金币不可达
        if(coin > amount)
            continue;
        int subProb = coinChange(coins, amount - coin);
        // 子问题无解
        if(subProb == -1)
            continue;
        // 每次找到最小的一个
        ans = min(ans, subProb + 1);
    }
    return (ans == INT_MAX) ? -1 : ans;

}

// 带备忘录的解法
int helper(vector<int> &coins, int amount, vector<int> &memo){
    if(amount == 0)
        return 0;
    if(memo[amount] != -2)
        return memo[amount];
    int ans = INT_MAX;
    for(int coin : coins){

        if(amount - coin < 0)
            continue;
        int subProb = helper(coins, amount - coin, memo);
        // 子问题无解
        if(subProb == -1)
            continue;
        ans = min(ans, subProb + 1);
    }
    memo[amount] = (ans == INT_MAX) ? -1 : ans;
    return memo[amount];
}

int coinChangePlus(vector<int> &coins, int amount){
    // 备忘录初始化为-2；
    vector<int> memo(amount + 1, -2);
    return helper(coins, amount, memo);
}

// 动态规划
int coinChangeDP(vector<int> &coins, int amount){
    // 初始化备忘录
    vector<int> memo(amount + 1, amount + 1);
    memo[0] = 0;
    // 填表
    for(int i = 1; i < memo.size(); i++){
        // 内层循环，找最小
        for(int coin : coins){
            if(i - coin < 0)
                continue;
            memo[i] = min(memo[i], memo[i - coin] + 1);
        }
    }
    return (memo[amount] == amount + 1) ? -1 : memo[amount];
}

int main()
{
    vector<int> coins;
    coins.push_back(1);
    coins.push_back(2);
    coins.push_back(5);
    cout<<coinChangeDP(coins, 11);
    return 0;
}