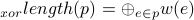acWing 144. 最长异或值路径

题面：

给定一个树，树上的边都具有权值。

树中一条路径的异或长度被定义为路径上所有边的权值的异或和：

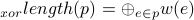
⊕ 为异或符号。

给定上述的具有n个节点的树，你能找到异或长度最大的路径吗？

输入格式

第一行包含整数n，表示树的节点数目。

接下来n-1行，每行包括三个整数u，v，w，表示节点u和节点v之间有一条边权重为w。

输出格式

输出一个整数，表示异或长度最大的路径的最大异或和。

数据范围

1≤n≤1000001≤n≤100000,
0≤u,v<n0≤u,v<n,
0≤w<2310≤w<231

输入样例：

4
0 1 3
1 2 4
1 3 6

输出样例：

7

样例解释

样例中最长异或值路径应为0->1->2,值为7 (=3 ⊕ 4)

 题解：

我们不妨设置一个数组D[x]表示根节点到x的路径上所有的边权的xor值,那么很显然,D[x]=D[father(x)] xor weight(x,father(x)) 也就是D[x节点的父亲]异或上x节点到他父亲的路径.既然如此的话,我们明显发现这道题目D数组是可以通过深度优先搜索求出.
求出所有的D数组,那么x节点到y节点上所有的异或权值就是D[x] xor D[y],换句话来说就是,从根节点到x节点的xor值,和根节点到y节点的xor值,这两条路径重叠了,然后这两条路径就抵消了,因为a xor a=0.本身和本身xor值是0的.
因此我们原问题就转换成为D[1]~D[n]中选择任意两个数,xor的结果值就会变成最大.也就是上一道题目.

代码：

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
int a[100010];
int h[100010],e[200010],c[200010],ne[200010],cnt;
int son[3000100][2],idx;
void add(int u,int v,int w)
{
    e[cnt]=v;c[cnt]=w;ne[cnt]=h[u];h[u]=cnt++;
}
void dfs(int u,int father,int sum)
{
 a[u]=sum;
 for(int i=h[u];i!=-1;i=ne[i])
 {
     int j=e[i];
     if(j!=father)dfs(j,u,sum^c[i]);
 }
}
void insert(int x)
{
    int p=0;
    for(int i=30;i>=0;i--)
    {
        int &s=son[p][x>>i&1];
        if(!s)s=++idx;
        p=s;
    }
}
int query(int x)
{
    int res=0,p=0;
    for(int i=30;i>=0;i--)
    {
        int s=x>>i&1;
        if(son[p][!s])
        {
            p=son[p][!s];
            res+=1<<i;
        }
        else
        p=son[p][s];
    }
    return res;
}
int main()
{
    memset(h,-1,sizeof h);
    int n;scanf("%d",&n);
    for(int i=0;i<n-1;i++)
     {
        int u,v,w;cin>>u>>v>>w;
        add(u,v,w);
        add(v,u,w);
     }
     dfs(0,-1,0);
     int res=0;
     //for(int i=0;i<n;i++)cout<<a[i]<<endl;
     for(int i=0;i<n;i++)insert(a[i]);
     for(int i=0;i<n;i++)res=max(res,query(a[i]));
     cout<<res<<endl;
    return 0;
}