法线从object space到eye space的转换((normal matrix)

　　对于顶点来说,从object Space转换到eye space, 使用model-view矩阵就好了.那么顶点的法线是否也可以直接使用model-view矩阵转化?

　　通常情况下是不行的.

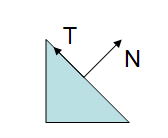
　　如下两张图是顶点的tangent和normal向量使用m-v矩阵从object space到eye space的变换:

　　>>>>>>>>>>>>>>>>  

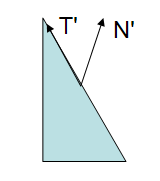
　　可以看到在eye-space中,tangent的方向仍符合定义,normal则不再垂直于tangent了.m-v矩阵不适用于normal.

　　令T为tangent,MV为model-view矩阵.P1, P2为tangent联系的2个顶点.

　　T = P2 - P1

　　T' = T * MV = (P2 - P1) * MV = P2 * MV - P1 * MV = P2' - P1'

　　因此T'保留了tangent的定义.但对于normal,你也可以找到N=Q2-Q1代表它,但是变换后Q2'-Q1'却不能保证垂直于T'.object space到view space,角度关系被改变了.

　　如何求出normal的变换,维持与tangent垂直?假设该变换为G.

　　normal与tangent垂直:
　　N'.T' = (GN).(MT) = 0

　　点积转化为叉积:

　　(GN).(MT) = (GN)^T * (MT) = (GN)^T(MT) =  (N^TG^T)(MT) = N^TG^TMT = 0

　　注意到N^TT为0:

　　若G^TM = I,则上式成立.因此G=(M^-1)^T.

　　即normal matrix是model-view矩阵的逆矩阵的转置矩阵.

　　若model-view矩阵是一个正交矩阵,则G=M.这便是例外情况下normal matrix为model-view矩阵.