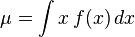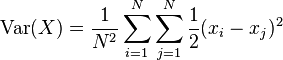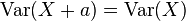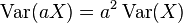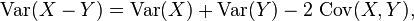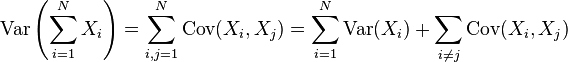方差var，标准差

wiki摘录如下(红色字体是特别标注的部分)：

方差：http://zh.wikipedia.org/wiki/%E6%96%B9%E5%B7%AE

方差

变异量（数）（Variance），应用数学里的专有名词。在概率论和统计学中，一个随机变量的方差描述的是它的离散程度，也就是该变量离其期望值的距离。一个实随机变量的方差也称为它的二阶矩或二阶中心动差，恰巧也是它的二阶累积量。方差的算术平方根称为该随机变量的标准差。

标准差才是变量离其期望值的距离，方差应该是距离的平方

以下的所有定义，都有平均值EX,其实在实际中很多时候会先将变量去中心化，也就是让变量的均值为0。带着这个想法看下面的定义，公式会变得更加简洁一些。

目录

  [隐藏] 

• 1 定义
  • 1.1 连续随机变量
  • 1.2 离散随机变量
• 2 特性
• 3 一般化
• 4 历史
• 5 参考出处
• 6 相关条目

定义

设X为服从分布F的随机变量， 如果E[X]是随机变量X的期望值（平均数μ=E[X]）
随机变量X或者分布F的方差为：

这个定义涵盖了连续、离散、或两者都有的随机变量。方差亦可当作是随机变量与自己本身的协方差：

方差典型的标记有Var(X),　,　或是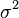，其表示式可展开成为：

上述的表示式可记为"平方的平均减掉平均的平方"

连续随机变量

如果随机变量X是连续分布，并对应至概率密度函数f(x)，则其方差为：

此处是一期望值，

且此处的积分为以X为范围的x定积分（definite integral）
如果一个连续分布不存在期望值，如柯西分布（Cauchy distribution），也就不会有方差。

离散随机变量

如果随机变量X是具有概率质量函数的离散概率分布x₁ ↦ p₁, ..., x_n ↦ p_n，则：

此处是其期望值, i.e.

 .

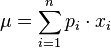当X为有N个相等概率值的平均分布：

N个相等概率值的方差亦可以点对点间的方变量表示为：

特性

方差不会是负的，因为次方计算为正的或为零：

一个常数随机变量的方差为零，且当一个资料集的方差为零时，其内所有项目皆为相同数值：

方差不变于定位参数的变动。也就是说，如果一个常数被加至一个数列中的所有变量值，此数列的方差不会改变：

如果所有数值被放大一个常数倍，方差会放大此常数的次方倍：

两个随机变量合的方差为：

此数Cov(., .)代表协方差。

对于个随机变量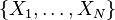的总和：

在样本空间Ω上存在有限期望和方差的随机变量构成一个希尔伯特空间： L²（Ω, dP），不过这里的内积和长度跟方差，标准差还是不大一样。 所以，我们得把这个空间“除”常变量构成的子空间，也就是说把相差一个常数的 所有原来那个空间的随机变量做成一个等价类。这还是一个新的无穷维线性空间， 并且有一个从旧空间内积诱导出来的新内积，而这个内积就是方差

一般化

如果X是一个向量其取值范围在实数空间Rⁿ，并且其每个元素都是一个一维随机变量，我们就把X称为随机向量。随机向量的方差是一维随机变量方差的自然推广，其定义为E[(X − μ)(X − μ)^T]，其中μ = E(X)，X^T是X的转置。这个方差是一个非负定的方阵，通常称为协方差矩阵。

如果X是一个复数随机变量的向量（向量中每个元素均为复数的随机变量），那么其方差定义则为E[(X − μ)(X − μ)^*]，其中X^*是X的共轭转置向量或称为埃尔米特向量。根据这个定义，变异数为实数。