回归模型定义:
1、回归分析是预测性建模技术,主要用来研究因变量(yi)与自变量(xi)之间的关系,通常被用来做预测分析、时间序列等。
2、公式:h(xi) = wxi + b = ∑j = 1wjxj + b
3、实质为根据过去的经验学习中学习出这些权重系数wj和偏置常数b各自取多少才能使得回归预测的准确度更高。
4、使用最小化损失函数进行求解。(最小均方误差)
5、使用梯度下降法对损失函数求偏导数。求出最小均方误差。
线性回归的sklearn实现
在scikit-learn中,线性回归模型对应的是liner_model.LinearRegression ,除此之外还有基于L1正则化的Lasso回归(Lasso Regression),基于L2正则化的线性回归(Ridge Regression),以及基于L1与L2正则化融合的Lasso CNet(ElasticNet Regression)中对应的linear_model.Lasso 、linear_model.Ridge 、linear_model.ElasticNet 。
普通线性回归:
from sklearn import linear_model linear_model.LinearRegression(fit_intercept = True ,normalize = False ,n_jobs = -1)
参数:
fit_intercept:选择是否计算偏置常数b,默认为True ,表示计算
normalize:选择在拟合数据前是否进行归一化,默认为False ,表示不进行归一化
n_jobs:表示所有cpu核都调用
属性:
coef_:用于输出线性回归模型的权重向量w
intercept_:用于输出线性回归模型的偏置常数b
方法:
fit(X_train ,y_train):进行模型训练
score(X_test ,y_test):返回模型在测试集上的预测准确率
Lasso回归:
from sklearn import linear_model linear_model.Lasso(alpha=1.0 , fit_intercept=True , normalize=False , precompute=False ,
max_iter=1000 , tol=0.0001 , warm_start=False , positive=False , selection='cyclic')
参数:
alpha:L1正则化项前面带的常数调节因子
fit_intercept:选择是否计算偏置常数b,默认为True ,表示计算
normalize:选择在拟合数据前是否进行归一化,默认为False ,表示不进行归一化
precompute:选择是否使用预先计算的Gram矩阵来加快计算,默认为False
max_iter:设定最大迭代次数,默认为1000次
tol:设定判断迭代收斂函数,默认为0.0001
warm_start:设定是否使用前一次训练的结果继续训练,默认为False,表示每次从头开始训练
positive:默认为False,如果为True,则强制所有权重系数都为正值
select:每轮迭代时选择哪个权重系数进行更新,默认为cycle ,表示从前往后依次选择;如果设定为random,则表示每次随机选择一个权重系数进行更新
属性:
coef_:用于输出线性回归模型的权重向量w
intercept_:用于输出线性回归模型的偏置常数b
n_iter_:用于输出实际迭代的次数
方法:
fit(X_train ,y_train):进行模型训练
score(X_test ,y_test):返回模型在测试集上的预测准确率
predict(X):用训练好的模型来预测待预测数据集X,返回数据为预测集对应的预测结果yˆ
岭回归:
岭回归的实质是在基本线性回归模型基础上添加L2正则化,使得各个特征的权重wj尽量衰减,从而达到特征变量选择的目的。
linear_model.Ridge(alpha=1.0 , fit_intercept=True , normalize=False , max_iter=None , tol=0.001 , solver='auto')
参数:
alpha:L1正则化项前面带的常数调节因子
fit_intercept:选择是否计算偏置常数b,默认为True ,表示计算
normalize:选择在拟合数据前是否进行归一化,默认为False ,表示不进行归一化
precompute:选择是否使用预先计算的Gram矩阵来加快计算,默认为False
max_iter:设定最大迭代次数,默认为1000次
tol:设定判断迭代收斂函数,默认为0.0001
solver:指定问题最优化问题的算法,默认为auto,表示自动选择。其他方法:
1、svd:使用奇异值分解来计算回归系数
2、cholesky:使用标准的scipy.linalg.solve函数来求解
3、sparse_cg:使用scipy.sparse.linalg.cg中的共轭梯度求解器求解
4、lsqr:使用专门的正则化最小二乘法scipy.sparse.ligalg.lsqr,速度是最快的
5、sag:使用随机平均梯度下降法求解
属性:
coef_:用于输出线性回归模型的权重向量w
intercept_:用于输出线性回归模型的偏置常数b
n_iter_:用于输出实际迭代的次数
方法:
fit(X_train ,y_train):进行模型训练
score(X_test ,y_test):返回模型在测试集上的预测准确率
predict(X):用训练好的模型来预测待预测数据集X,返回数据为预测集对应的预测结果yˆ
ElasticNet回归:
ElasticNet回归(弹性网络回归)是将L1和L2正则化进行融合,在基本的线性回归模型中加入混合正则化项。
linear_model.ElasticNet(alpha=1.0 , l1_ratio=0.5 , fit_intercept=True , normalize=False , precompute=False , max_iter=1000 , tol=0.0001 , warm_start=False , positive=False , selection='cyclic')
参数:
alpha:L1正则化项前面带的常数调节因子
l1_ratio:参数是β值,默认为0.5
fit_intercept:选择是否计算偏置常数b,默认为True ,表示计算
normalize:选择在拟合数据前是否进行归一化,默认为False ,表示不进行归一化
precompute:选择是否使用预先计算的Gram矩阵来加快计算,默认为False
max_iter:设定最大迭代次数,默认为1000次
tol:设定判断迭代收斂函数,默认为0.0001
warm_start:设定是否使用前一次训练的结果继续训练,默认为False,表示每次从头开始训练
positive:默认为False,如果为True,则强制所有权重系数都为正值
selection:每轮迭代时选择哪个权重系数进行更新,默认为cycle ,表示从前往后依次选择;如果设定为random,则表示每次随机选择一个权重系数进行更新
属性:
coef_:用于输出线性回归模型的权重向量w
intercept_:用于输出线性回归模型的偏置常数b
n_iter_:用于输出实际迭代的次数
方法:
fit(X_train ,y_train):进行模型训练
score(X_test ,y_test):返回模型在测试集上的预测准确率
predict(X):用训练好的模型来预测待预测数据集X,返回数据为预测集对应的预测结果yˆ
案例之波士顿房价预测
#导入数据 from sklearn.datasets import load_boston boston = load_boston() X = boston.data y = boston.target #划分训练测试 from sklearn.model_selection import train_test_split X_train ,X_test ,y_train ,y_test = train_test_split(X ,y ,train_size = 0.7)
普通线性回归模型:
from sklearn.linear_model import LinearRegression lr = LinearRegression() lr.fit(X_train ,y_train) lr.score(X_test ,y_test)

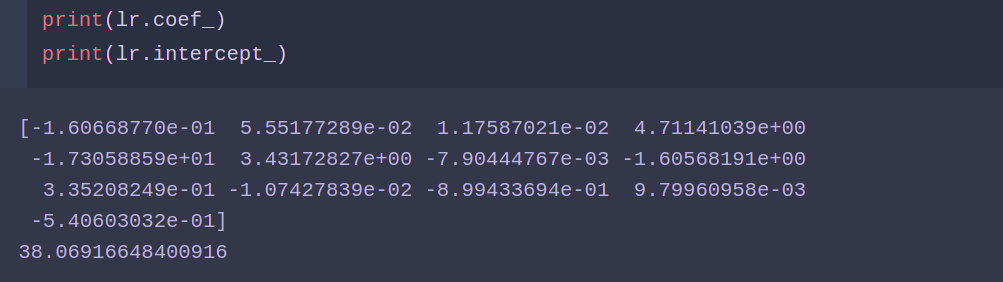
lasso模型:
from sklearn.linear_model import Lasso las = Lasso() las.fit(X_train ,y_train) las.score(X_test ,y_test)

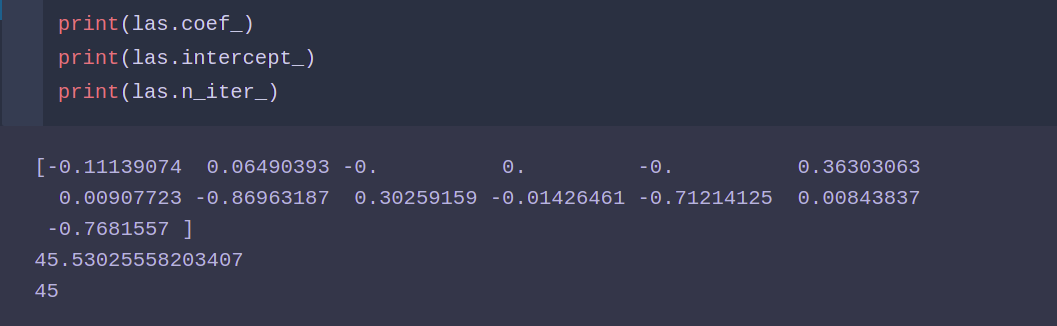
岭回归模型:
from sklearn.linear_model import Ridge rdg = ElasticNet() rdg.fit(X_train ,y_train) rdg.score(X_test ,y_test)

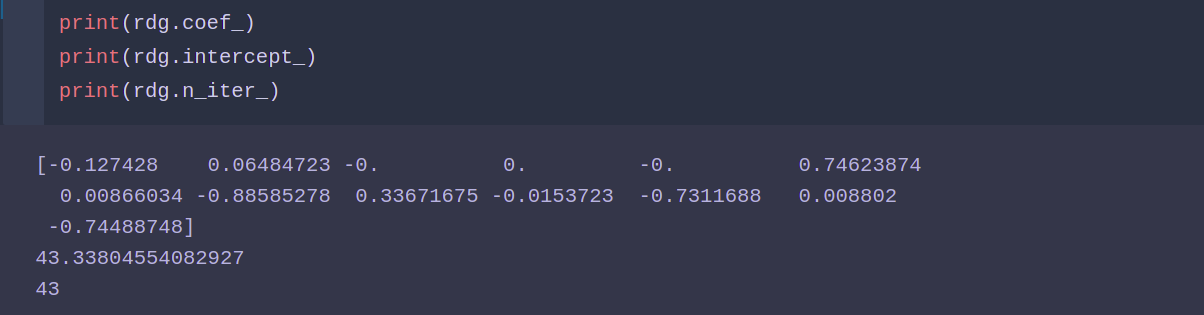
ElasticNet模型:
from sklearn.linear_model import ElasticNet elt = ElasticNet() elt.fit(X_train ,y_train) elt.score(X_test ,y_test)

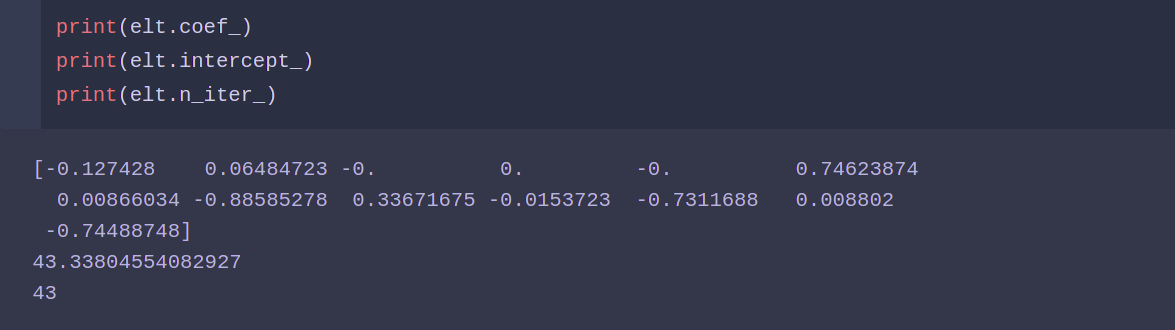
画图表现:
import matplotlib.pyplot as plt fig = plt.figure(figsize=(20,3)) axes = fig.add_subplot(1,1,1) line1 = axes.plot(range(len(y_test)) ,y_test ,'b' ,label = 'Actual') elt_result = elt.predict(X_test) line2 = axes.plot(range(len(elt_result)) ,elt_result ,'r--' ,label = 'Predict' ,linewidth = 2) axes.grid() fig.tight_layout() plt.legend(handles = line1) plt.title('House Price') plt.show()
