Luogu P1640 [SCOI2010]连续攻击游戏|二分图

Luogu P1640 [SCOI2010]连续攻击游戏|二分图

题意：给定(n)个装备，每个装备有两个属性值，每种装备只能使用其中一个属性，并且每个装备只能用一次。现在要从属性(1)开始，依次使用装备，问最多能使用多少个。

题解：

二分图。我不会告诉你是因为从试炼场进来才想到的

建模很巧妙，我们可以以属性为左端点（属性值(le n)），装备为右端点做二分图匹配。以样例为例，是这样的。

3
1 2
3 2
4 5

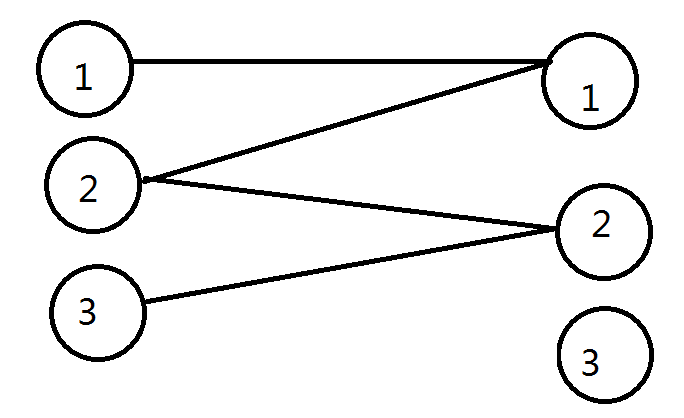
显然，(4),(5)不可能被使用，所以略去。

然后从(1)到(n)，按属性值匹配，这里匹配的意义已经很明显了。当属性(i)无法匹配时，输出(i-1)

我们的程序已经成形了，长这样

#include<bits/stdc++.h>
using namespace std;
int cc,to[2002000],net[2002000],fr[2002000];
int fa[2002000],vis[2002000],n,a,b;
void addedge(int u,int v)
{
    if (u>n) return ;
    cc++;
    to[cc]=v;net[cc]=fr[u];fr[u]=cc;
}
int findgf(int x)//匈牙利
{
    if (vis[x]) return false;
    vis[x]=true;
    for (int i=fr[x];i;i=net[i])
    {
        if (fa[to[i]])
        {
            if (findgf(fa[to[i]]))
            {
                fa[to[i]]=x;
                return true;
            }
        }
        else
        { 
            fa[to[i]]=x;
            return true;
        }
    }
    return false;
}
int main()
{
    cin>>n;
    for (int i=1;i<=n;i++)
    {
        cin>>a>>b;
        addedge(a,n+i);
        addedge(b,n+i);
    }
    for (int i=1;i<=n+1;i++)
    {
        for (int j=1;j<=n;j++)
          vis[j]=false;
        if (!findgf(i)) {cout<<i-1<<endl;break;}
    }
    return 0;
}

这里因为(for)循环清空数组，(TLE)了。

回想一下匈牙利算法，我们想到了一种优化。

当某一个已经连接某个点的左端点已经不可能连接其他右端点时，可以把(vis)直接置(true)，否则，在退出(dfs)时，将其置(false)。这样便不用每次初始化。

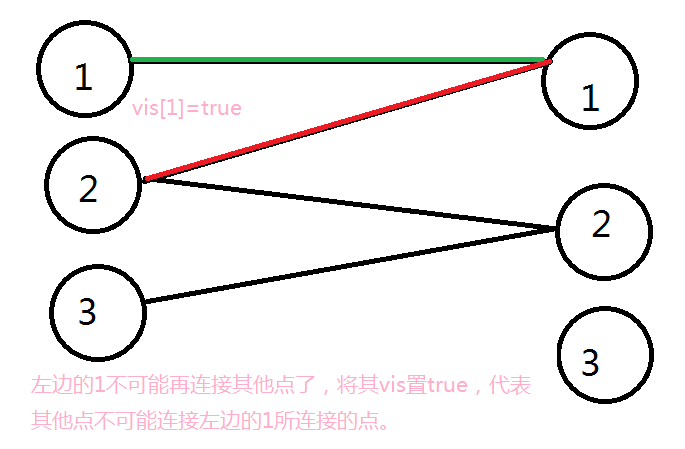
这个优化使我们的程序快多了，可以通过。

#include<bits/stdc++.h>
using namespace std;
int cc,to[2002000],net[2002000],fr[2002000];
int fa[2002000],vis[2002000],n,a,b;
void addedge(int u,int v)
{
    if (u>n) return ;
    cc++;
    to[cc]=v;net[cc]=fr[u];fr[u]=cc;
}
int findgf(int x)//匈牙利
{
    if (vis[x]) return false;
    vis[x]=true;
    for (int i=fr[x];i;i=net[i])
    {
        if (fa[to[i]])
        {
            if (findgf(fa[to[i]]))
            {
                fa[to[i]]=x;
                vis[x]=false;
                return true;
            }
        }
        else
        { 
            fa[to[i]]=x;
            vis[x]=false;
            return true;
        }
    }
    return false;
}
int main()
{
    cin>>n;
    for (int i=1;i<=n;i++)
    {
        cin>>a>>b;
        addedge(a,n+i);
        addedge(b,n+i);
    }
    for (int i=1;i<=n+1;i++)
    {
        if (!findgf(i)) {cout<<i-1<<endl;break;}
    }
    return 0;
}