机器学习中的MLE和MAP两大学派的争论:
频率学派 - Frequentist - Maximum Likelihood Estimation (MLE,最大似然估计):
频率学派认为世界是确定的,有一个本体,这个本体的真值是不变的,我们的目标就是要找到这个真值或真值所在的范围。
贝叶斯学派 - Bayesian - Maximum A Posteriori (MAP,最大后验估计):
贝叶斯学派认为世界是不确定的,人们对世界先有一个预判,而后通过观测数据对这个预判做调整,我们的目标是要找到最优的描述这个世界的概率分布。
在对事物建模时,用θ表示模型的参数,请注意,解决问题的本质就是求θ。那么:
频率学派:存在唯一真值θ。当数据量趋于无穷时,这种方法能给出精准的估计;然而缺乏数据时则可能产生严重的偏差。
贝叶斯学派: θ是一个随机变量,符合一定的概率分布。在贝叶斯学派里有两大输入和一大输出,输入是先验 (prior)和似然 (likelihood),输出是后验 (posterior)。
先验,即P(θ),指的是在没有观测到任何数据时对θ的预先判断,似然,即P(X|θ),是假设θ已知后我们观察到的数据应该是什么样子的;后验,即P(θ|X),是最终的参数分布。
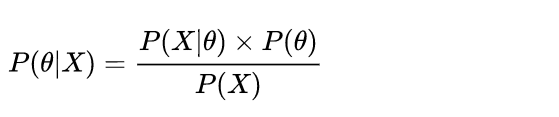
随着数据量的增加,参数分布会越来越向数据靠拢,先验的影响力会越来越小