1、HASH的基本概念
Hash,一般翻译做“散列”,也有直接音译为”哈希”的,就是把任意长度的输入(又叫做预映射,pre-image),通过散列算法,变换成固定长度的输出,该输出就是散列值。
这种转换是一种压缩映射,也就是,散列值的空间通常远小于输入的空间,不同的输入可能会散列成相同的输出,而不可能从散列值来唯一的确定输入值。
简单的说就是一种将任意长度的消息压缩到某一固定长度的消息摘要的函数。
HASH主要用于信息安全领域中加密算法,他把一些不同长度的信息转化成杂乱的128位的编码里,叫做HASH值.也可以说,hash就是找到一种数据内容和数据存放地址之间的映射关系
2、加密算法的介绍
(1)什么是MD5算法
MD5讯息摘要演算法(英语:MD5 Message-Digest Algorithm),一种被广泛使用的密码杂凑函数,可以产生出一个128位的散列值(hash value),用于确保信息传输完整一致。
MD5的前身有MD2、MD3和MD4。
(2)MD5功能
输入任意长度的信息,经过处理,输出为128位的信息(数字指纹);
不同的输入得到的不同的结果(唯一性);
(3)MD5算法的特点
- 压缩性:任意长度的数据,算出的MD5值的长度都是固定的
- 容易计算:从原数据计算出MD5值很容易
- 抗修改性:对原数据进行任何改动,修改一个字节生成的MD5值区别也会很大
- 强抗碰撞:已知原数据和MD5,想找到一个具有相同MD5值的数据(即伪造数据)是非常困难的。
(4)MD5算法是否可逆?
MD5不可逆的原因是其是一种散列函数,使用的是hash算法,在计算过程中原文的部分信息是丢失了的。
(5)MD5用途
-
防止被篡改:
-
比如发送一个电子文档,发送前,我先得到MD5的输出结果a。然后在对方收到电子文档后,对方也得到一个MD5的输出结果b。如果a与b一样就代表中途未被篡改。
-
比如我提供文件下载,为了防止不法分子在安装程序中添加木马,我可以在网站上公布由安装文件得到的MD5输出结果。
-
SVN在检测文件是否在CheckOut后被修改过,也是用到了MD5.
-
-
防止直接看到明文:
- 现在很多网站在数据库存储用户的密码的时候都是存储用户密码的MD5值。这样就算不法分子得到数据库的用户密码的MD5值,也无法知道用户的密码。
- (比如在UNIX系统中用户的密码就是以MD5(或其它类似的算法)经加密后存储在文件系统中。当用户登录的时候,系统把用户输入的密码计算成MD5值,然后再去和保存在文件系统中的MD5值进行比较,进而确定输入的密码是否正确。
- 通过这样的步骤,系统在并不知道用户密码的明码的情况下就可以确定用户登录系统的合法性。这不但可以避免用户的密码被具有系统管理员权限的用户知道,而且还在一定程度上增加了密码被破解的难度。)
-
防止抵赖(数字签名):
- 这需要一个第三方认证机构。例如A写了一个文件,认证机构对此文件用MD5算法产生摘要信息并做好记录。
- 若以后A说这文件不是他写的,权威机构只需对此文件重新产生摘要信息,然后跟记录在册的摘要信息进行比对,相同的话,就证明是A写的了。这就是所谓的“数字签名”。
SHA-1
安全哈希算法(Secure Hash Algorithm)主要适用于数字签名标准(Digital Signature Standard DSS)里面定义的数字签名算法(Digital Signature Algorithm DSA)。
对于长度小于2^64位的消息,SHA1会产生一个160位的消息摘要。当接收到消息的时候,这个消息摘要可以用来验证数据的完整性。
SHA是美国国家安全局设计的,由美国国家标准和技术研究院发布的一系列密码散列函数。
由于MD5和SHA-1于2005年被山东大学的教授王小云破解了,科学家们又推出了SHA224, SHA256, SHA384, SHA512,当然位数越长,破解难度越大,但同时生成加密的消息摘要所耗时间也更长。目前最流行的是加密算法是SHA-256 .
MD5与SHA-1的比较
由于MD5与SHA-1均是从MD4发展而来,它们的结构和强度等特性有很多相似之处,SHA-1与MD5的最大区别在于其摘要比MD5摘要长32 比特。
对于强行攻击,产生任何一个报文使之摘要等于给定报文摘要的难度:MD5是2128数量级的操作,SHA-1是2160数量级的操作。产生具有相同摘要的两个报文的难度:MD5是264是数量级的操作,SHA-1 是280数量级的操作。
因而,SHA-1对强行攻击的强度更大。但由于SHA-1的循环步骤比MD5多80:64且要处理的缓存大160比特:128比特,SHA-1的运行速度比MD5慢。
3、Python的 提供的相关模块
import hashlib
m = hashlib.md5()#定义
m.update(b"Hello")#转化
m.update(b"It's me")
print(m.digest())#输出
m.update(b"It's been a long time since last time we ...")
print(m.digest()) #2进制格式hash
print(len(m.hexdigest())) #16进制格式hash
'''
def digest(self, *args, **kwargs): # real signature unknown
""" Return the digest value as a string of binary data. """
pass
def hexdigest(self, *args, **kwargs): # real signature unknown
""" Return the digest value as a string of hexadecimal digits. """
pass
import hashlib
# ######## md5 ########
hash = hashlib.md5()
hash.update('admin')
print(hash.hexdigest())#输出16进制
# ######## sha1 ########
hash = hashlib.sha1()
hash.update('admin')
print(hash.hexdigest())
# ######## sha256 ########
hash = hashlib.sha256()
hash.update('admin')
print(hash.hexdigest())
# ######## sha384 ########
hash = hashlib.sha384()
hash.update('admin')
print(hash.hexdigest())
# ######## sha512 ########
hash = hashlib.sha512()
hash.update('admin')
print(hash.hexdigest())
4、网络上的密码破解拓展知识
比如支付宝,数据库里面存的密码是我们的密码的md5值,数据库泄露了也没事,没有储存我们的明文密码
密码破解网站:http://www.cmd5.com/
举例:
m = hashlib.md5()
m.update(b'xiao')
print(m.hexdigest())
>d2bf7126723ea8f6005ba141ea3c3e2c
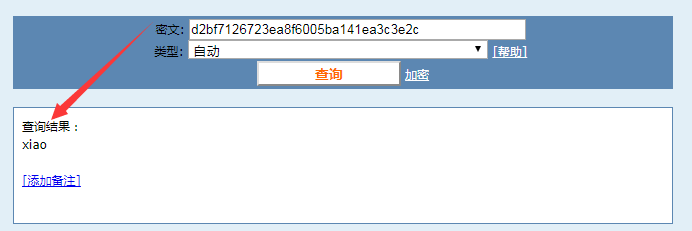
我把得到的密码:xiao 的md5值输入可以反解出我的明文密码:xiao
现在我把密码复杂化:
m = hashlib.md5() m.update(b'xiao&@,12') print(m.hexdigest())
df9fd762077060eb80c8b4d2ddb2aeed
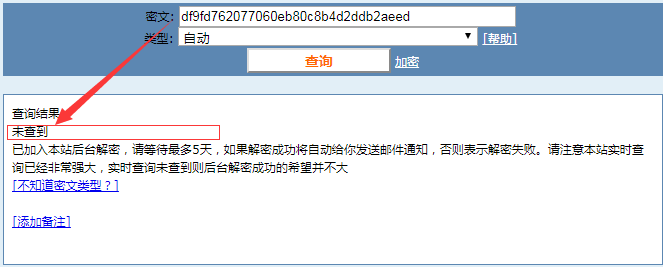
这个并不是破解了,而是运用撞库的原理
先在数据库里存了很多明文,各种排列组合,对应的md5值,拿到md5值后去撞库有匹配成功的就输出,
所以我们在设置密码的时候尽量要复杂化