Description:
给定一个nxm的网格,请计算三点都在格点上的三角形共有多少个。下图为4x4的网格上的一个三角形。注意三角形的三点不能共线。
n,m<=1000
再整理一下题解的思路:
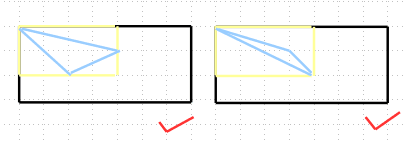
首先 把我们要找的三角形刚好框到一个矩形里
也就是说在这个矩形的边上任意找两点连线一定能把三角形分成两部分
可以发现 对于各种不同的子矩形 找框在其中的三角形数量的方法是一样的(后面再讲)
所以我们现在的任务就是求子矩形的数量
题解里是这样做的:可以发现我们并不关心矩形在哪里 所以不必要枚举起点终点
我们只关心矩形的长x宽y以及这样的矩形有多少个
所以枚举x,y 矩形数为(n-x+1)*(m-y+1)
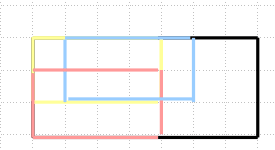
(n-x+1)*(m-y+1)这个式子是如何得到的呢 画图就知道啦(下图)
把黄色矩形平移得到蓝色的 红色的 etc.很好理解
然后现在我们就把问题转化为了给定知道长宽的矩形 求框在里面的三角形数
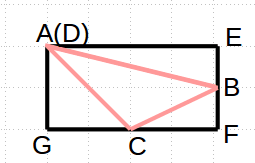
现在就要分类讨论啦用ABC来表示三角形,x为AE的长,y为AG的长
首先很容易知道的是 三角形的一顶点一定在矩形的顶点上 令这点为A
1. B,C 两点都不在顶点上,则B一定在EF上 C一定在FG上,且A可以取在四个顶点
所以这种情况的方案数为 4*(x-1)*(y-1)
2.B与E重合 方案数为x-1
3.C与G重合 方案数为y-1
2,3两种情况其实就是三角形有两个顶点在矩形顶点上且相连不是对角线
所以2,3的方案数之和为2*(x-1+y-1)
4.B或C与F重合 不妨取B与F重合
这时C可以取矩形里的任何格点(先不考虑三点共线 )
则方案数为(x+1)*(y+1)
然后我们要减掉三点共线的情况 也就是求AB经过的格点数(包括本身)
AB经过的格点数为 gcd(x,y)+1
原因:(不严谨请指出,因为题解没证 我自己想的)
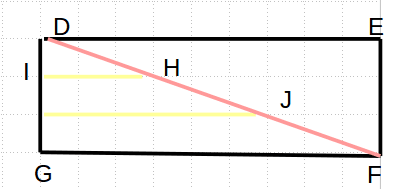
如图,矩形对角线DF经过四个格点
除本身以外,取经过的点中最上方的点H向DG作垂线垂足为I
则三角形DHI一定相似于三角形DGF
然后我们发现 y/DI-1即为经过的格点数(除A,B) 我们只要求出DI即可
设DI为z 则x/y*z(即为HI)必定为整数
又要z最小 所以z=y/gcd(x,y) 则y/z=gcd(x,y)
综上 长为x宽为y的矩形的对角线经过的格点个数为 gcd(x,y)+1
又因为矩形的对角线有两条
所以最后这种情况的方案数为2*[(x+1)*(y+1)-gcd(x,y)-1]
把几种情况的方案数加起来 为 4*(x-1)*(y-1)+2(x-1+y-1)+2*[(x+1)*(y+1)-gcd(x,y)-1]
化简之后为6*x*y-2*gcd(x,y)
CODE:
 View Code1 #include<iostream> 2 #include<cstdio> 3 #define R register 4 #define go(i,a,b) for(R int i=a;i<=b;i++) 5 #define ll long long 6 using namespace std; 7 int read() 8 { 9 int x=0,y=1;char c=getchar(); 10 while(c<'0'||c>'9') {if(c=='-') y=-1;c=getchar();} 11 while(c>='0'&&c<='9') {x=(x<<1)+(x<<3)+c-'0';c=getchar();} 12 return x*y; 13 } 14 ll ans,n,m; 15 int gcd(int x,int y) 16 { 17 return x%y==0?y:gcd(y,x%y); 18 } 19 int main() 20 { 21 n=read();m=read(); 22 go(i,1,n) go(j,1,m) ans+=(n-i+1)*(m-j+1)*(6*i*j-2*gcd(i,j)); 23 printf("%lld",ans); 24 return 0; 25 }
View Code1 #include<iostream> 2 #include<cstdio> 3 #define R register 4 #define go(i,a,b) for(R int i=a;i<=b;i++) 5 #define ll long long 6 using namespace std; 7 int read() 8 { 9 int x=0,y=1;char c=getchar(); 10 while(c<'0'||c>'9') {if(c=='-') y=-1;c=getchar();} 11 while(c>='0'&&c<='9') {x=(x<<1)+(x<<3)+c-'0';c=getchar();} 12 return x*y; 13 } 14 ll ans,n,m; 15 int gcd(int x,int y) 16 { 17 return x%y==0?y:gcd(y,x%y); 18 } 19 int main() 20 { 21 n=read();m=read(); 22 go(i,1,n) go(j,1,m) ans+=(n-i+1)*(m-j+1)*(6*i*j-2*gcd(i,j)); 23 printf("%lld",ans); 24 return 0; 25 }