$Poj3017 Cut The Sequence$ 单调队列优化$DP$

 Poj   AcWing

Description

给定一个长度为N的序列 A,要求把该序列分成若干段,在满足“每段中所有数的和”不超过M的前提下,让“每段中所有数的最大值”之和最小.

N<=10⁵,M<=10¹¹,0<Ai<=10⁶

Sol

一篇比较清楚的题解 $OvO$

$F[i]$表示把前$i$个数分成若干段,满足每段中所有数之和不超过$M$的前提下,各段的最大值之和的最小值

不难推出转移方程:

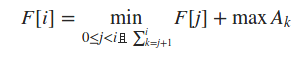
 但是直接枚举$j$的做法是$O(N^{2})$的,显然过不去,还要优化.

DP转移优化的指导思想是及时排除不可能的决策,保持候选集合的高度有效性和秩序性.

本着这个思想我们来思考怎样的j可能成为最优解.

$j$要满足一下两个条件之一才有可能成为最优解:

1.$A[j+1]=max Ak$

2.$sum_{k=j}^{i}Ak>M$ 即: j是满足区间和小于等于$M$的最小下标

证明,反证法:

假设以上条件都不成立

由以上条件可知$[j,i]$和$[j-1,i]$的区间都是满足题意(区间和$<=M$)且区间最大值相等

又因为显然有$F[j-1]$≤$F[j]$

所以$F[j-1]+max{Ak}<F[j]+max{Ak}$

$j-1$比$j$更优,$j$不可能是最优的

第$1$个条件显然可以维护一个$j$递增,$Aj$递减的单调队列

第$2$个条件的$j$也显然是递增的,所以就维护一个$nw$表示对于当前i满足该条件的$j$,$i+1$时,检查$nw$是否还满足区间和$>M$,满足就$nw++$.至于$max Ak$,当然可以用$ST$表预处理出来,但是其实不用辣么麻烦,因为对于每一个$i$,我们都会算出满足条件$1$ 的 $j$,然后它就是最大值丫,就可以直接更新答案了.

Code

#include<iostream>
#include<cstdio>
#define il inline
#define Rg register
#define go(i,a,b) for(Rg int i=a;i<=b;i++)
#define yes(i,a,b) for(Rg int i=a;i>=b;i++)
#define ll long long
using namespace std;
il int read()
{
    int x=0,y=1;char c=getchar();
    while(c<'0'||c>'9'){if(c=='-')y=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+c-'0';c=getchar();}
    return x*y;
}
int n,a[100001],q[100001],f[100001];
ll m,s[100001];
int main()
{
    n=read(),scanf("%lld",&m);
    go(i,1,n){a[i]=read();s[i]=s[i-1]+a[i];if(a[i]>m){printf("-1");return 0;}}
    int nw=1,h=1,t=0;
    go(i,1,n)
    {
        while(s[i]-s[nw-1]>m)nw++;
        while(h<=t && q[h]<nw)h++;
        while(h<=t && a[q[t]]<=a[i])t--;
        q[++t]=i;
        f[i]=f[nw-1]+a[q[h]];
        go(j,h,t-1)f[i]=min(f[i],f[q[j]]+a[q[j+1]]);
    }
    printf("%d
",f[n]);
    return 0;
}