DP----入门的一些题目(POJ1088 POJ1163 POJ1050)

动态规划入门 DP 基本思想 具体实现 经典题目 POJ1088 POJ1163 POJ1050

(一) POJ1088，动态规划的入门级题目。嘿嘿，连题目描述都是难得一见的中文。

题目分析：

求最长的滑雪路径，关键是确定起点，即从哪开始滑。

不妨设以( i, j )为起点，现在求滑行的最长路径。

首先，( i, j )能滑向的无非就是它四周比它低的点。到底滑向哪个点？很简单，谁长滑行谁。假设(i, j )--->( i, j+1 ), 现在就变成了：以( i, j+1 )为起点，求最长滑行路径的问题。这样一直下去，直到某个局部最低点，就算滑行结束了。

状态转换方程：

dp( i,j ) = Max( dp( i-1, j ), dp( i, j+1 ),dp( i+1, j ), dp( i, j-1 ) ) + 1;

其中：dp( i,j )表示以( i, j )为起点，所能滑行的最长长度 

编程实现：

枚举起点，找到最长的滑行路径。因为涉及到上下左右的点，所以注意边界情况的处理。还是记忆化递归来的简便，直接把Invalid的情况给剪掉。

 

(二) POJ1163，DP的入门级题目。和上面的POJ1088有些相似，也可以看成从上往下滑。不过起点是确定的，只能( 1, 1 )开始。

 题目分析：

要使和最大，关键是确定终点。不妨设以( i, j )为起点，现在求滑行的最长路径。

如果( i, j )为终点，则前一个点只可能是( i-1, j-1 )或者( i-1, j )。选择的标准，还是看哪个点更优。如果假设( i, j )--->( i-1, j-1 )，则问题又变成了：以( i-1, j-1 )为终点求最大和的问题。

 状态转换方程：

dp( i,j ) = Max( dp( i-1, j-1 ), dp( i-1, j) ) + data[i][j];

其中：dp( i,j )表示以( i, j )为终点，所得到的最大和。

data[i][j]表示三角矩阵中第i行第j列的值

 编程实现：

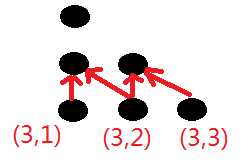
同样，要注意三角矩阵的边界。边界的有些点不能用状态方程就去。如图2所示，(3,1)和(3,3)要单独处理。

(三) POJ1050，动态规划必做题目，经典程度五颗星。这个题目的前身就是：求最大子序列和。

      先来看最大子序列和。有一串数，有正有负，如2，-1，5，4，-9，7，0，3，-5。求：这一串数中，和最大的一段。比如说，从第一个数2开始，发现下一个为-1，加下-1后和显然会变小。再往后看，第三个数是5，所以上一个-1还是要选的，这样才能加上5。哎，不看了，这样求最大和还不得累死。嘿嘿，这时DP就派上用场了。

 

设这串数为X1 X2 X3 … Xn, 用dp(i,j)表示从Xi…Xj的最大子序列和。

按照DP的思路，想办法减小问题的规模。有n个数，怎样能减少到n-1数？想办法把最后一个数Xn去掉，问题规模就能减少到n-1。

通过观察可以发现：X1…Xn的最大子序列可以分为两类：以Xn结尾、不以Xn结尾。不以Xn结尾的最大子序列，其实就是X1…Xn-1的最大子序列，发现这点很重要。

这样就有：dp( i, j ) = Max( dp( i, j-1 ), Last( j ) ).其中Last( j )表示以Xj结尾的最大子序列的和。

功夫不负有心人，终于把问题规模减少了。但是，一波未平一波又起，新的问题又出现了。Last( j )如何求？即，求以Xj结尾的最大子序列的和。再用DP求解。

Last( j )和Last( j-1 )之间的关系比较简单。Last(j )的值里面必然会包括Xj的值，到底有没有Last( j-1 )也很简单，主要取决于Last( j-1 )是正还是负。

这样就有：Last( j ) = Max( Xj,  Last( j-1) + Xj );

 状态转换方程：

dp( i, j ) = Max( dp( i, j-1 ), Last( j ) )其中：dp(i,j)表示从Xi…Xj的最大子序列和

Last( j ) = Max( Xj, Last( j-1 ) + Xj ); 其中：Last( j )表示以Xj结尾的最大子序列的和

 

       现在，回到POJ1050。想想能不能利用上面的结果？求最大子矩阵，那么只要确定了子矩阵有几行、几列即可。这样，可以枚举子矩阵的行数和列数。

比如，当子矩阵只要一行时，那么只关心它的列从哪开始到那结束就行。哦，这其实就是一个最大子序列和的问题。这一行就是这一串数，求和最大的一段。那么当子矩阵有两行时，怎么办？如何把两行变为一行？一个聪明的想法就是：把这两行按照对应的列加起来。

好了问题已经漂亮的解决了：在原矩阵中任意画出一部分，然后按照对应的列加起来，问题就转变为一个最大子序列和的问题

POJ1088

#include <iostream>
using namespace std;

//***********************常量定义*****************************

const int MAX = 105;


//*********************自定义数据结构*************************




//********************题目描述中的变量************************

int row;
int col;
int data[MAX][MAX];
int max(int a,int b){
	return a>b?a:b;
}

//**********************算法中的变量**************************

//dp[i][j]表示从data[i][j]出发所能滑行的最大长度
int dp[MAX][MAX];


//***********************算法实现*****************************


int DP( int r, int c )
{
	//如果已经计算过，则直接返回
	if( dp[r][c] > 0 ) return dp[r][c];
	
	int ans = 0;
	int tmp = 0;

	//只对有效的r、c进行计算
	if( r - 1 >= 1 )
	{
		//剪枝：只能滑行更低的点
		if( data[r][c] > data[r-1][c] )
		{
		 ans =max( DP( r-1, c ),ans);
		}					
	}
	if( r + 1 <= row )
	{
		if( data[r][c] > data[r+1][c] )
		{
			ans =max( DP( r+1, c ),ans);
		}
	}
	if( c - 1 >= 1 )
	{
		if( data[r][c] > data[r][c-1] )
		{
		ans =max( DP( r, c-1 ),ans);
		}
	}
	if( c + 1 <= col )
	{
		if( data[r][c] > data[r][c+1] )
		{
			ans =max( DP( r, c+1 ),ans);
		}
	}
	
	//如果是普通点，由状态转换方程
	//DP(i,j) = max( DP(i,j-1), DP(i,j+1), DP(i-1,j), DP(i+1,j) ) + 1;
	//如果是某个局部最低点，则返回 0 + 1 = 1
	dp[r][c] = ans + 1;
	return dp[r][c];
	
}

void Solve()
{
	int ans = 0;
	for( int i=1; i<=row; i++ )
	{
		for( int j=1; j<=col; j++ )
		{
			 ans =max( DP(i,j), ans);			
		}
	}
	cout << ans << endl;
}


//************************main函数****************************

int main()
{
	

	cin >> row >> col;
		memset(dp,0,sizeof(dp));
	for( int i=1; i<=row; i++ )
	{
		for( int j=1; j<=col; j++ )
		{
			cin >> data[i][j];
		}
	}	
	Solve();		
	return 0;
}

边界处理还有另一种方法;貌似用时更短

#include<iostream>
#include<string.h>
using namespace std;
const int MAX=105;
int graph[MAX][MAX],w[MAX][MAX];
int direction[4][2]={{-1,0},{0,1},{1,0},{0,-1}};////////////////////////////////////////////注意这
int R,C;

int DP(int _x,int _y){
	if(w[_x][_y]!=0) return w[_x][_y];
	int maxn=0,s;
	for(int i=0;i<4;i++){
		int x=_x+direction[i][0],y=_y+direction[i][1];/////////////////////////////////////////////和这
		if(x>=0&&x<R&&y>=0&&y<C&&graph[x][y]<graph[_x][_y]){
			s=DP(x,y);
			if(s>maxn) maxn=s;}}
	w[_x][_y]=maxn+1;
	return maxn+1;
}

int main(){
	while(~scanf("%d%d",&R,&C)){
		int ans=-1;memset(w,0,sizeof(w));
		for(int i=0;i<R;i++)
			for(int j=0;j<C;j++)
				scanf("%d",&graph[i][j]);
		for(int i=0;i<R;i++)
			for(int j=0;j<C;j++){
				w[i][j]=DP(i,j);
				if(w[i][j]>ans) ans=w[i][j];}
		printf("%d
",ans);
	}
	return 0;
}

POJ1163

#include <iostream>
using namespace std;

//***********************常量定义*****************************

const int MAX_ROW_NUM = 105;


//*********************自定义数据结构*************************




//********************题目描述中的变量************************

int rowNum;
int data[MAX_ROW_NUM][MAX_ROW_NUM];


//**********************算法中的变量**************************

//pathSum[i][j]表示起点(1,1)终点(i,j)的最长路径的长度值
int pathSum[MAX_ROW_NUM][MAX_ROW_NUM];


//***********************算法实现*****************************

inline int Larger( int x, int y )
{
	return ( x > y ) ? x : y;
}

void Solve()
{
	//设置初值，三角矩阵前两行单独处理
	pathSum[1][1] = data[1][1];
	pathSum[2][1] = pathSum[1][1] + data[2][1];
	pathSum[2][2] = pathSum[1][1] + data[2][2];
	
	int r, c;
	for( r=3; r<=rowNum; r++ )
	{
		//对每行第一列单独处理
		pathSum[r][1] = pathSum[r-1][1] + data[r][1];

		//根据状态转换方程计算
		for( c=2; c<=r-1; c++ )
		{
			pathSum[r][c] = Larger( pathSum[r-1][c], pathSum[r-1][c-1] )  + data[r][c];
		}
		
		//对每行最后一列单独处理
		pathSum[r][r] = pathSum[r-1][r-1] + data[r][r];
	}

	int max = 0;
	for( int i=1; i<=rowNum; i++ )
	{
		max = Larger( max, pathSum[rowNum][i] );
	}
	cout << max << endl;
}


//************************main函数****************************

int main()
{
	//freopen( "in.txt", "r", stdin );		
	
	cin >> rowNum;
	for( int i=1; i<=rowNum; i++ )
	{
		for( int j=1; j<=i; j++ )
		{
			cin >> data[i][j];
		}
	}

	Solve();
	return 0;
}

POJ1050

#include <iostream>
using namespace std;

//***********************常量定义*****************************

const int MAX_ROW_NUM = 105;


//*********************自定义数据结构*************************




//********************题目描述中的变量************************

int rowNum;
int data[MAX_ROW_NUM][MAX_ROW_NUM];


//**********************算法中的变量**************************

//pathSum[i][j]表示起点(1,1)终点(i,j)的最长路径的长度值
int pathSum[MAX_ROW_NUM][MAX_ROW_NUM];


//***********************算法实现*****************************

inline int Larger( int x, int y )
{
	return ( x > y ) ? x : y;
}

void Solve()
{
	//设置初值，三角矩阵前两行单独处理
	pathSum[1][1] = data[1][1];
	pathSum[2][1] = pathSum[1][1] + data[2][1];
	pathSum[2][2] = pathSum[1][1] + data[2][2];
	
	int r, c;
	for( r=3; r<=rowNum; r++ )
	{
		//对每行第一列单独处理
		pathSum[r][1] = pathSum[r-1][1] + data[r][1];

		//根据状态转换方程计算
		for( c=2; c<=r-1; c++ )
		{
			pathSum[r][c] = Larger( pathSum[r-1][c], pathSum[r-1][c-1] )  + data[r][c];
		}
		
		//对每行最后一列单独处理
		pathSum[r][r] = pathSum[r-1][r-1] + data[r][r];
	}

	int max = 0;
	for( int i=1; i<=rowNum; i++ )
	{
		max = Larger( max, pathSum[rowNum][i] );
	}
	cout << max << endl;
}


//************************main函数****************************

int main()
{
	//freopen( "in.txt", "r", stdin );		
	
	cin >> rowNum;
	for( int i=1; i<=rowNum; i++ )
	{
		for( int j=1; j<=i; j++ )
		{
			cin >> data[i][j];
		}
	}

	Solve();
	return 0;
}

版权声明：本文为博主原创文章，未经博主允许不得转载。