本文作者frankchenfu,blogs网址http://www.cnblogs.com/frankchenfu/,转载请保留此文字。
数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。通常情况下,精心选择的数据结构可以带来更高的运行或者存储效率。数据结构往往同高效的检索算法和索引技术有关。
不过,作为一些刚刚接触数据结构的人来说,我们并不需要了解这么多——恰恰相反,我们从简单的开始。
这里,我先讲的的基本的树。
最基本的树,是比较简单的。它长的就像生活中的树一样——有树根,有枝条(分支),有叶子……。不过,在计算机中,我们一般把它倒过来: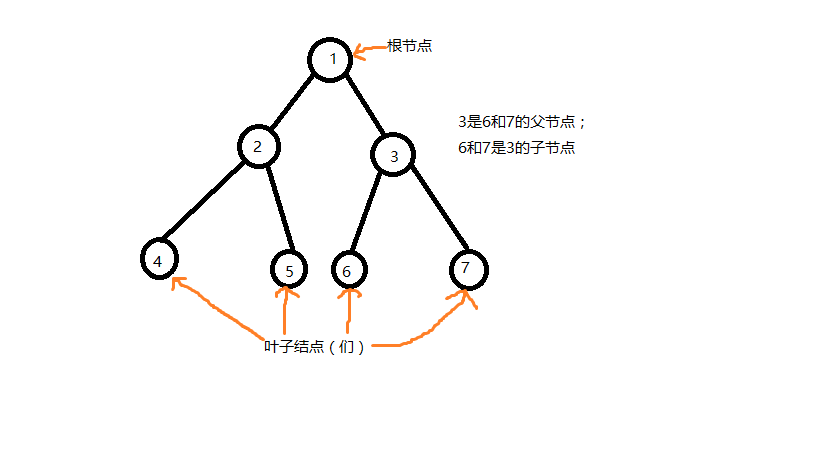
我图画的丑,别怪我。
然后一些基本的名词,例如根节点,叶子结点,父节点及子节点等,有大概能理解了吧。
上面的树叫二叉树,每个非叶子节点的结点都最多只有两个孩子 。
树一般这么定义:
struct tree
{
int num;
struct tree *left;
struct tree *right;
};
left指向左儿子,right指向右儿子,num表示该节点的值(?)。当然,也可以直接用数组模拟,数组模拟虽然可能不好理解,但是代码复杂度略低 。
插入一个结点就是找到他的父亲,让父亲的左儿子或者右儿子指向他。删除比较复杂,暂时不讨论。
struct tree father; struct tree son; struct tree *p=&father; father.left=&son; *p->left;
接下来,我们设想一下,如果我们给这个树上的每一个结点赋予一个值(存在上面的num里!)……然后,我们在经过调整后,使得这个二叉树有序,那么会怎么样呢?
还是上面的那张图,假设编号为1的结点的值就是1,编号为2的结点值就是2……那么上面的树是不是满足一个性质:每个父节点的值都比它所有的孩子的值小?
答案是肯定的(不信你自己看),那么这个就是一个二叉堆。再仔细点来说,这是一个小根堆。(什么大根小根的!)
小根堆指的是每个父节点的值都比它所有的孩子的值小;相反,大根堆指的是每个父节点的值都比它所有的孩子的值大。
我们来做一个模拟,看一看如何插入新节点。
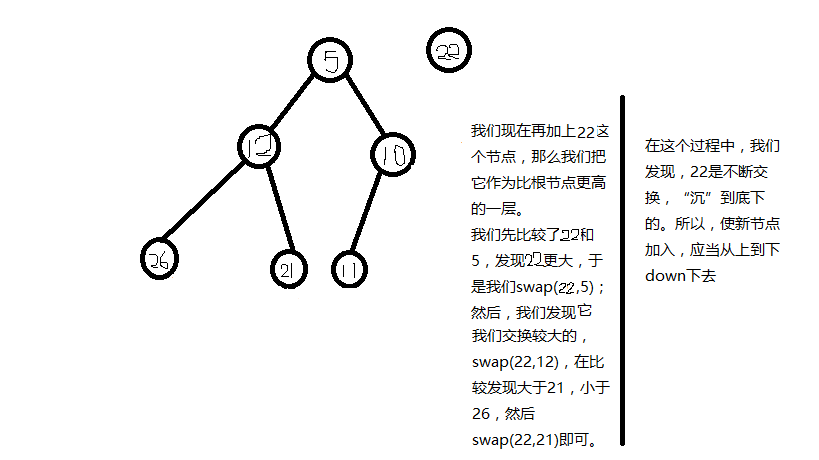
所以,根据这个原理,我们就能“维护”堆,使它始终满足堆的性质。然后,我们用数组模拟法,实现小根堆。Cpp代码:
#include<cstdio> const int MAX=1001; int a[MAX]; void swap(int *a,int *b) { int t=*a; *a=*b; *b=t; } void down(int i,int m) { int x; while((i<<1)<=m) { i<<=1; if((i<m)&&(a[i+1]>a[i])) i++; if(a[i]>a[i>>1]) swap(&a[i],&a[i>>1]); else break; } } int main() { int n; scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&a[i]); for(int i=n>>1;i>=1;i--) down(i,n); for(int i=n;i>=2;i--) { swap(&a[i],&a[1]); down(1,i-1); } for(int i=1;i<=n;i++) printf("%d ",a[i]); return 0; }
然后,我们看到,输出是有序的——无论你输入是否有序。这就是传说中的堆排序。但是这不是正宗的,他只是类似于一个叫优先队列的东西。
堆在STL里也有模板(其实是优先队列,不过大多数时候可以用)。下面是常见的。
#include<queue>
using namespace std;
priority_queue<int>a;
int main()
{
a.push(10);
a.pop();
a.size();
a.empty();
}
这篇文章到这就结束了,希望对大家有所帮助,谢谢!