人老了,学东西有点慢,学了一天,真是尴尬。
参考:http://www.cnblogs.com/wuminye/p/3525957.html
http://dongxicheng.org/structure/lca-rmq/
LCA算法就是求一棵有根树上两个结点(假设是S、T点)的最近的祖先。
我用的是基于 RMQ 的算法来做的。(RMQ 是什么?我迟点再补上吧。。)
这个算法的思想呢就是,把这棵树看成是一个无向图,然后求S和T之间的最短路径,然后,他们的最近公共祖先肯定在这条路上。(显而易见吧~)
然后再想想,他们的公共祖先有什么特点???是不是这条路径中深度最小的那个结点?(是不是很有道理??)
好了,深度最小,那么我们就可以直接用RMQ来查询了 ( 开什么玩笑,在树上怎么用RMQ!!!你个骗纸!!!)
是路径啊喂!!!路径就是一个数组嘛,怎么不可以RMQ了!!!!(可是怎么多路径,怎么搞啊!!!)
好了,问题来了,这么路径,怎么RMQ呢????
我们先想一下,对一棵树进行DFS的时候,顺序是怎样的?
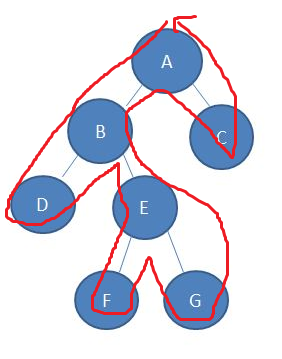
比如上面这个图,遍历的时候
顺序应该是 A B D B E F E G E B A C A
然后深度是 0 1 2 1 2 3 2 3 2 1 0 1 0
举例:
比如 D到C的最短路径 : DBAC 在上面序列中对应的是 D B E F E G E B A C
比如D到G的最短路径:DBEG 在上面序列中对应的是 D B E F E G
都是首尾一样,中间不太一样,然后再看看深度,发现中间多的那部分,深度都没有比最近祖先更小的!!!
所以,上面这个序列就是我们想要的啊!!!! 找到起点跟终点就可以进行RMQ查询了!!!
HDOJ 2586 AC 代码
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 const int maxn = 1e5 + 10; 5 // pos 存首次出现的位置 R存结点深度 idarr存遍历后的序列 6 int pos[maxn], R[maxn], idarr[maxn<<1]; 7 bool vis[maxn]; 8 int tot, n; 9 int rmq[maxn<<1][20], dis[maxn]; 10 void ST() { 11 memset(rmq, 0, sizeof(rmq)); 12 for(int i=1; i<=tot; i++) rmq[i][0] = idarr[i]; 13 for(int j=1; j<20; j++) { 14 for(int i=1; i<=tot; i++) { 15 if(i+(1<<(j-1)) > tot) break; 16 int a = rmq[i][j-1], b = rmq[min(i+(1<<(j-1)), tot)][j-1]; 17 rmq[i][j] = R[a] < R[b] ? a : b; 18 } 19 } 20 } 21 int query(int l, int r) { 22 int t = (int)log2(r-l+1.5); 23 int a = rmq[l][t], b = rmq[r-(1<<t)+1][t]; 24 return R[a] < R[b] ? a : b; 25 } 26 struct Edge 27 { 28 int to, rev, cost; 29 }; 30 std::vector<Edge> G[maxn]; 31 void add(int u, int v, int cost) { 32 G[u].push_back((Edge){v, (int)G[v].size(), cost}); 33 swap(u, v); 34 G[u].push_back((Edge){v, (int)G[v].size()-1, cost}); 35 } 36 void dfs(int u, int dept) { 37 vis[u] = true; 38 idarr[++tot] = u; 39 pos[u] = tot; 40 R[u] = dept; 41 for(unsigned i=0; i<G[u].size(); i++) { 42 if(vis[G[u][i].to]) continue; 43 dis[G[u][i].to] = dis[u] + G[u][i].cost; 44 dfs(G[u][i].to, dept + 1); 45 idarr[++tot] = u; 46 } 47 } 48 int main() { 49 int T, m; 50 scanf("%d", &T); 51 while(T--) { 52 scanf("%d%d", &n, &m); 53 int a, b, c; 54 for(int i=1; i<n; i++) { 55 scanf("%d%d%d", &a, &b, &c); 56 add(a, b, c); 57 } 58 memset(dis, 0, sizeof(dis)); 59 memset(R, 0, sizeof(R)); 60 memset(vis, 0, sizeof(vis)); 61 tot = 0; 62 dfs(1, 0); 63 ST(); 64 while(m--) { 65 scanf("%d%d", &a, &b); 66 if(pos[a] > pos[b]) swap(a, b); 67 int t = query(pos[a], pos[b]); 68 printf("%d ", dis[a]+dis[b]-2*dis[t]); 69 } 70 for(int i=0; i<maxn; i++) G[i].clear(); 71 } 72 return 0; 73 }