C++Directx11开发笔记六:3D空间坐标系变换,绘制3D图形动画
上一篇文章中我们认识了Direct3D中一些空间坐标系,其中包含了几何模型坐标系,世界坐标系,观察坐标系,投影坐标系以及屏幕坐标系,一些纯理论的知识。今天我们来了解一下这些坐标系的变换,并且通过一个例子来说明这些坐标系的关系。这些变换主要在于几何模型到世界坐标系的变化,世界坐标系到观察坐标系的变化,和观察坐标系到投影之间的变换,最后将投影所得的图像通过绘图管线在屏幕上绘制出来。
世界坐标系转换:
世界坐标系转换其实就是将顶点从几何模型坐标系移到世界坐标系中,在游戏里就是构建游戏场景,将物品放置到一个场景里。通常在世界坐标系转换时,还将通过改变大小来控制基元物件的放大或缩小,通过改变方向来设置旋转,通过改变位置来进行转变。在一个场景中,每一个物件都有他自己的世界坐标系转换矩阵,这是由于每一个物件都有其自己的大小,方向和位置。
观察坐标系转换:
所有顶点在转换到世界坐标系后,观察坐标系转换将其从世界坐标系转换为观察坐标系中。前面我们讲过,观察坐标系即是在世界坐标系内,从观测者或者摄像机角度透视所能够看到的图像,在观察坐标系内,观测者将站在原点(或者说以观测者为原点),透视的方向即是Z轴方向,即观察方向为Z轴方向。
很值得注意的是,虽然观察坐标空间是从观测者在世界坐标系内所能够看到的一个框架,但是观察坐标系矩阵却是由定点来填充的,而非观测者。因此,观察矩阵所填充的数据是和观测者或者摄像机里的正好相反,比如说,我们想把摄像机往-z方向移动4个单位,那么我们必须计算出观察矩阵转换的定点正好为4个单位的Z轴方向。虽然摄像机是往反方向移动,但是在摄像机里的成像却是相反的。在Direct3D中有一个方法可以用来计算这种观察矩阵,那就是XMMatrixLookAtLH()方法,我们只要告诉他观测者的位置,所观看的位置,并且告诉他观察者向上方向,就可以计算出观察矩阵。
投影坐标系转换:
投影坐标系转换即是将定点从3D坐标系如:世界和观察坐标系转换为投影坐标系,在投影坐标系中,一个顶点的X和Y坐标是根据在3D空间中的X/Z和Y/Z的比率获得的。首先我们来看一个图,那样有助于我们理解这个概念,如下所示:
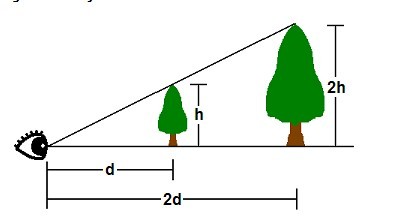
在3D中,根据透视法,越靠*的物体越大,从上图可以看出,一棵高为h单位在远离观测点d单位的树,和一棵高为2h单位距离观测点2d位置的树是一样大的。因此,顶点在2D屏幕上呈现是依据X/Z和Y/Z的比率决定的。
在Direct3D中以一个叫做FOV(field-of-view),这个主要是通过特定方向判断特定位置的顶点是否可见。每个人都有一个FOV,当然那是在我们的前方,因为我们不可能看到后面,如果两个物体离得太*或非常远也是看不到的。在计算机绘图里,FOV包含在一个视截体里,在3D中这个视截体被定义一个六面体,有两个面是XY面*行,他们被叫做*Z视*面和远Z视*面。其它的面被定义为观测者的横向和纵向可视界面,FOV越大,视截体的体积也越大,当然容纳的物体也更多,如下图所示。

GPU会过滤视截体外部的东东以至于不会浪费那些不需要显示的部分,这个被称为裁剪,GPU将会将顶点转换为投影顶点,那样就可以知道是否在视截体内。在Direct3D 11中,这些换行都被一个方法完成,那就是XMMatrixPerspectiveFovLH(),我们将提高4个参数,FOVy,比率,Zn和Zf即可以获得投影矩阵。其中FOVy就是Y方向的投影角度,比率就是宽和高比率,Zn和Zf分别是*视面和远视面的大小。
绘制3D图形:
有了以上理论知识,我们就可以在屏幕上绘制3D图形了。在前面的例子中我们学会了如何绘制三角形,这里我们将绘制一个立方体。根据我们前面的例子知道,计算机绘图中需要告诉GPU三角形的顶点,因此我们需要先定义一下立方体的顶点,由于立方体有8个顶点,所以我们可以定义一个数组。并且我们还需要告诉像素着色器颜色,因此我们可以先定义一个结构,其代码如下:
{
XMFLOAT3 Pos;
XMFLOAT4 Color;
};
SimpleVertex vertices[] =
{
{ XMFLOAT3( -1.0f, 1.0f, -1.0f ), XMFLOAT4( 0.0f, 0.0f, 1.0f, 1.0f ) },
{ XMFLOAT3( 1.0f, 1.0f, -1.0f ), XMFLOAT4( 0.0f, 1.0f, 0.0f, 1.0f ) },
{ XMFLOAT3( 1.0f, 1.0f, 1.0f ), XMFLOAT4( 0.0f, 1.0f, 1.0f, 1.0f ) },
{ XMFLOAT3( -1.0f, 1.0f, 1.0f ), XMFLOAT4( 1.0f, 0.0f, 0.0f, 1.0f ) },
{ XMFLOAT3( -1.0f, -1.0f, -1.0f ), XMFLOAT4( 1.0f, 0.0f, 1.0f, 1.0f ) },
{ XMFLOAT3( 1.0f, -1.0f, -1.0f ), XMFLOAT4( 1.0f, 1.0f, 0.0f, 1.0f ) },
{ XMFLOAT3( 1.0f, -1.0f, 1.0f ), XMFLOAT4( 1.0f, 1.0f, 1.0f, 1.0f ) },
{ XMFLOAT3( -1.0f, -1.0f, 1.0f ), XMFLOAT4( 0.0f, 0.0f, 0.0f, 1.0f ) },
};
注:三角带用于连接所有顶点,形带状, 顶点索引才指定用各点构成的三角形覆盖。
我们知道,GPU识别的最小几何单位是三角形(点线除外),我们告诉GPU立方体的顶点是绘制不出来的,所以我们要转换一下。立方体有6个面,也就是12个三角形,那就是有36个顶点,上面我们才定义了八个顶点,是不是不够呢?前面一章节我们也知道,多边形可以共用一边,即共用两个顶点,因此我们可以通过定义一个索引来描述顶点,其代码如下:
{
3,1,0,
2,1,3,
0,5,4,
1,5,0,
3,4,7,
0,4,3,
1,6,5,
2,6,1,
2,7,6,
3,7,2,
6,4,5,
7,4,6,
};
上面的数字就是表示vertices的下标,8个顶点就是0-7。创建索引缓存和创建顶点缓存很像,顶点缓存前面已经描述过就不再写了,创建索引缓存如下:
ZeroMemory( &bd, sizeof(bd) );
bd.Usage = D3D11_USAGE_DEFAULT;
bd.ByteWidth = sizeof( WORD ) * 36; // 36 vertices needed for 12 triangles in a triangle list
bd.BindFlags = D3D11_BIND_INDEX_BUFFER;
bd.CPUAccessFlags = 0;
bd.MiscFlags = 0;
InitData.pSysMem = indices;
if( FAILED( g_pd3dDevice->CreateBuffer( &bd, &InitData, &g_pIndexBuffer ) ) )
return FALSE;
创建了索引缓存后需要灌水GPU这个索引缓存,那样他才知道如何使用,其代码如下:
万事具备,当然接下来我们要确定的就是坐标系的确立,将其移动到世界坐标系内,我们先看一下如下代码:
XMMATRIX g_World;
XMMATRIX g_View;
XMMATRIX g_Projection;
//初始化
// Initialize the world matrix
g_World = XMMatrixIdentity();
// Initialize the view matrix
XMVECTOR Eye = XMVectorSet( 0.0f, 1.0f, -5.0f, 0.0f );
XMVECTOR At = XMVectorSet( 0.0f, 1.0f, 0.0f, 0.0f );
XMVECTOR Up = XMVectorSet( 0.0f, 1.0f, 0.0f, 0.0f );
g_View = XMMatrixLookAtLH( Eye, At, Up );
// Initialize the projection matrix
g_Projection = XMMatrixPerspectiveFovLH( XM_PIDIV2, width / (FLOAT)height, 0.01f, 100.0f );
从上面的代码中可以确立顶点坐标矩阵的确立,为了更能够突出3维的效果,我们先让他转动起来,即通过游戏时间让立方体绕自己的Y轴移动某个角度,其方法为:XMMatrixRotationY。其主要代码如下所示:
// Update variables
//
ConstantBuffer cb;
cb.mWorld = XMMatrixTranspose( g_World );
cb.mView = XMMatrixTranspose( g_View );
cb.mProjection = XMMatrixTranspose( g_Projection );
g_pImmediateContext->UpdateSubresource( g_pConstantBuffer, 0, NULL, &cb, 0, 0 );
//
// Renders a triangle
//
g_pImmediateContext->VSSetShader( g_pVertexShader, NULL, 0 );
g_pImmediateContext->VSSetConstantBuffers( 0, 1, &g_pConstantBuffer );
g_pImmediateContext->PSSetShader( g_pPixelShader, NULL, 0 );
g_pImmediateContext->DrawIndexed( 36, 0, 0 ); // 36 vertices needed for 12 triangles in a triangle list
