最近在GitHub上学习了有关python实现常见机器学习算法
目录
- 一、线性回归
1、代价函数
2、梯度下降算法
3、均值归一化
4、最终运行结果
5、使用scikit-learn库中的线性模型实现
- 二、逻辑回归
1、代价函数
2、梯度
3、正则化
4、S型函数
5、映射为多项式
6、使用的优化方法
7、运行结果
8、使用scikit-learn库中的逻辑回归模型实现
- 逻辑回归_手写数字识别_OneVsAll
1、随机显示100个数字
2、OneVsAll
3、手写数字识别
4、预测
5、运行结果
6、使用scikit-learn库中的逻辑回归模型实现
- 三、BP神经网络
1、神经网络model
2、代价函数
3、正则化
4、反向传播BP
5、BP可以求梯度的原因
6、梯度检查
7、权重的随机初始化
8、预测
9、输出结果
- 四、SVM支持向量机
1、代价函数
2、Large Margin
3、SVM Kernel
4、使用中的模型代码
5、运行结果
- 五、K-Mearns聚类算法
1、聚类过程
2、目标函数
3、聚类中心的选择
4、聚类个数K的选择
5、应用——图片压缩
6、使用scikit-learn库中的线性模型实现聚类
7、运行结果
- 六、PCA主成分分析（降维）
1、用处
2、2D-->1D,nD-->kD
3、主成分分析PCA与线性回归的区别
4、PCA降维过程
5、数据恢复
6、主成分个数的选择（即要降的维度）
7、使用建议
8、运行结果
9、使用scikit-learn库中的PCA实现降维
- 七、异常检测Anomaly Detection
1、高斯分布（正态分布）
2、异常检测算法
3、评价的好坏，以及
的选取
4、选择使用什么样的feature（单位高斯分布）
5、多元高斯分布
6、单元和多元高斯分布特点
7、程序运行结果
一、线性回归
1、代价函数
其中
。
下面就是求出theta，使代价最小，即代表我们拟合出来的方程距离真实值最近共有m条数据，其中
代表我们拟合出来的方程到真实值距离的平方，平方的原因是因为可能有负值，系数2的原因是下面求梯度是对每个变量求偏导，2可以消去。
代码实现：
1 # 计算代价函数 2 def computerCost(X,y,theta): 3 m = len(y) 4 J = 0 5 J = (np.transpose(X*theta-y))*(X*theta-y)/(2*m) #计算代价J 6 return J
注意这里的X是真实数据前加了一列1，因为有theta(0)
2、梯度下降算法
代价函数对
求偏导得到：
所以对theta的更新可以写成：
其中
为学习速率，控制梯度下降的速度，一般取0.01，0.03，0.1，0.3......
为什么梯度下降可以逐步减小代价函数？
假设函数f(x)的泰勒展开：f(x+△x)=f(x)+f'(x)*△x+o(△x),令:△x=-α*f'(x),即负梯度方向乘以一个很小的步长α，将△x带入泰勒展开式中：
f(x+x)=f(x)-α*[f'(x)]²+o(△x)
可以看出，α是取得很小的正数，[f'(x)]²也是正数，所以可以得出f(x+△x)<=f(x)，所以沿着负梯度放下，函数在减小，多维情况一样。
1 # 梯度下降算法 2 def gradientDescent(X,y,theta,alpha,num_iters): 3 m = len(y) 4 n = len(theta) 5 temp = np.matrix(np.zeros((n,num_iters))) # 暂存每次迭代计算的theta，转化为矩阵形式 6 J_history = np.zeros((num_iters,1)) #记录每次迭代计算的代价值 7 8 for i in range(num_iters): # 遍历迭代次数 9 h = np.dot(X,theta) # 计算内积，matrix可以直接乘 10 temp[:,i] = theta - ((alpha/m)*(np.dot(np.transpose(X),h-y))) #梯度的计算 11 theta = temp[:,i] 12 J_history[i] = computerCost(X,y,theta) #调用计算代价函数 13 print '.', 14 return theta,J_history
3、均值归一化
均值归一化的目的是使数据都缩放到一个范围内，便于使用梯度下降算法
其中
为所有此feature数据的平均值，
可以为此feature的最大值减去最小值，也可以为这个feature对应的数据的标准差。
代码实现：
1 # 归一化feature 2 def featureNormaliza(X): 3 X_norm = np.array(X) #将X转化为numpy数组对象，才可以进行矩阵的运算 4 #定义所需变量 5 mu = np.zeros((1,X.shape[1])) 6 sigma = np.zeros((1,X.shape[1])) 7 8 mu = np.mean(X_norm,0) # 求每一列的平均值（0指定为列，1代表行） 9 sigma = np.std(X_norm,0) # 求每一列的标准差 10 for i in range(X.shape[1]): # 遍历列 11 X_norm[:,i] = (X_norm[:,i]-mu[i])/sigma[i] # 归一化 12 13 return X_norm,mu,sigma
注意预测的时候也需要均值归一化数据
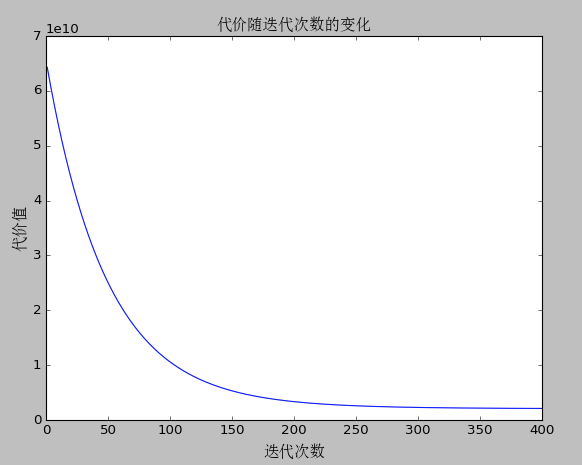
4、最终运行结果
代价随迭代次数的变化
5、使用scikit-learn库中的线性模型实现
1 #-*- coding: utf-8 -*- 2 import numpy as np 3 from sklearn import linear_model 4 from sklearn.preprocessing import StandardScaler #引入归一化的包 5 6 def linearRegression(): 7 print u"加载数据... " 8 data = loadtxtAndcsv_data("data.txt",",",np.float64) #读取数据 9 X = np.array(data[:,0:-1],dtype=np.float64) # X对应0到倒数第2列 10 y = np.array(data[:,-1],dtype=np.float64) # y对应最后一列 11 12 # 归一化操作 13 scaler = StandardScaler() 14 scaler.fit(X) 15 x_train = scaler.transform(X) 16 x_test = scaler.transform(np.array([1650,3])) 17 18 # 线性模型拟合 19 model = linear_model.LinearRegression() 20 model.fit(x_train, y) 21 22 #预测结果 23 result = model.predict(x_test) 24 print model.coef_ # Coefficient of the features 决策函数中的特征系数 25 print model.intercept_ # 又名bias偏置,若设置为False，则为0 26 print result # 预测结果 27 28 29 # 加载txt和csv文件 30 def loadtxtAndcsv_data(fileName,split,dataType): 31 return np.loadtxt(fileName,delimiter=split,dtype=dataType) 32 33 # 加载npy文件 34 def loadnpy_data(fileName): 35 return np.load(fileName) 36 37 38 if __name__ == "__main__": 39 linearRegression()