矩阵加法就是相同位置的数字加一下,矩阵减法也类似
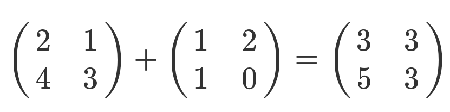
矩阵乘以一个常数,就是所有位置都乘以这个数
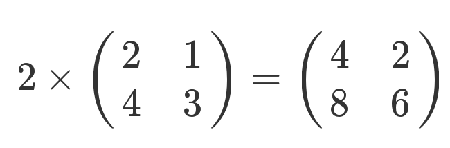
矩阵乘以矩阵
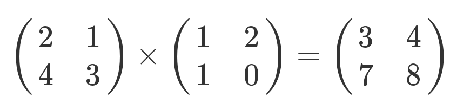
计算规则是,第一个矩阵第一行的每个数字(2和1),各自乘以第二个矩阵第一列对应位置的数字(1和1),然后将乘积相加( 2 x 1 + 1 x 1),得到结果矩阵左上角的那个值3
矩阵的本质就是线性方程式,两者是一一对应关系。如果从线性方程式的角度,理解矩阵乘法就毫无难度。下面是一组线性方程式
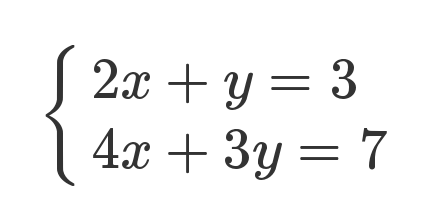
矩阵的最初目的,只是为线性方程组提供一个简写形式
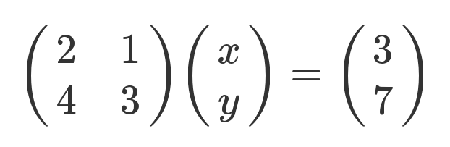
下面是严格的证明。有三组未知数 x、y 和 t,其中 x 和 y 的关系如下
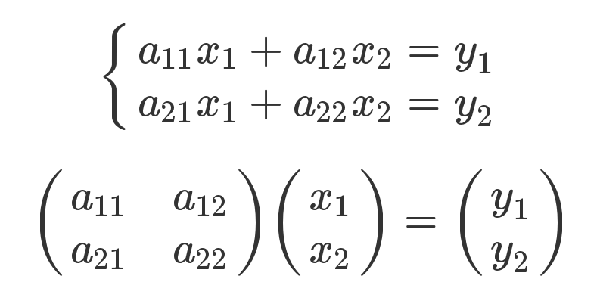
x 和 t 的关系如下
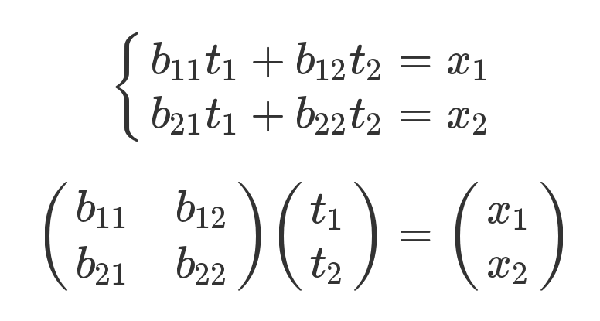
有了这两组方程式,就可以求 y 和 t 的关系。从矩阵来看,很显然,只要把第二个矩阵代入第一个矩阵即可
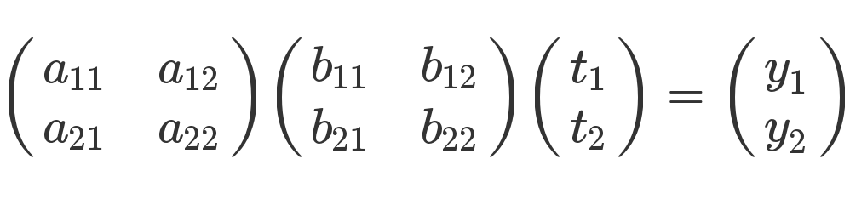
从方程式来看,也可以把第二个方程组代入第一个方程组
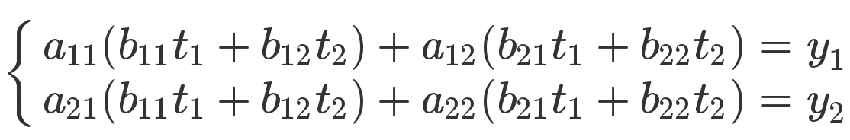
上面的方程组可以整理成下面的形式
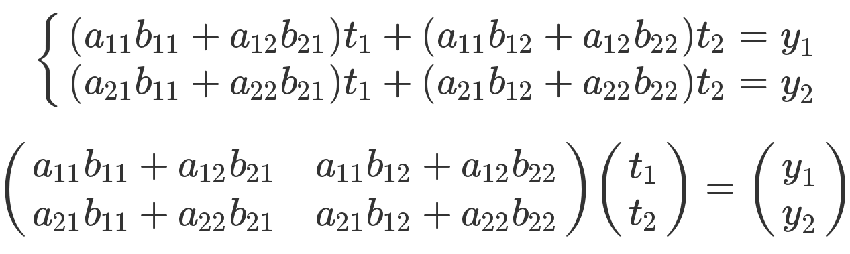
最后那个矩阵等式,与前面的矩阵等式一对照,就会得到下面的关系
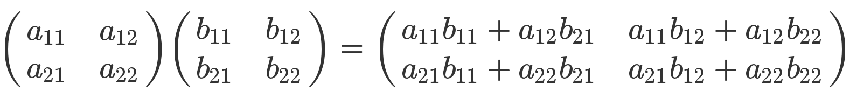
矩阵乘法的计算规则,从而得到证明