题目
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的数字可以无限制重复被选取。
- 所有数字(包括
target)都是正整数。 - 解集不能包含重复的组合。
分析
此题和 77题组合题目类似,又有区别。同一个数字可以无限制底被选取,意味着搜索的深度可能不确定,但是我们可以限制搜索的深度,即递归的终止条件是当前总和大于target。
题目又要求解集不存在重复组合,并且一个数可重复选取,那么每次递归时 startIndex就不必为 i 加一,直接为 i 。
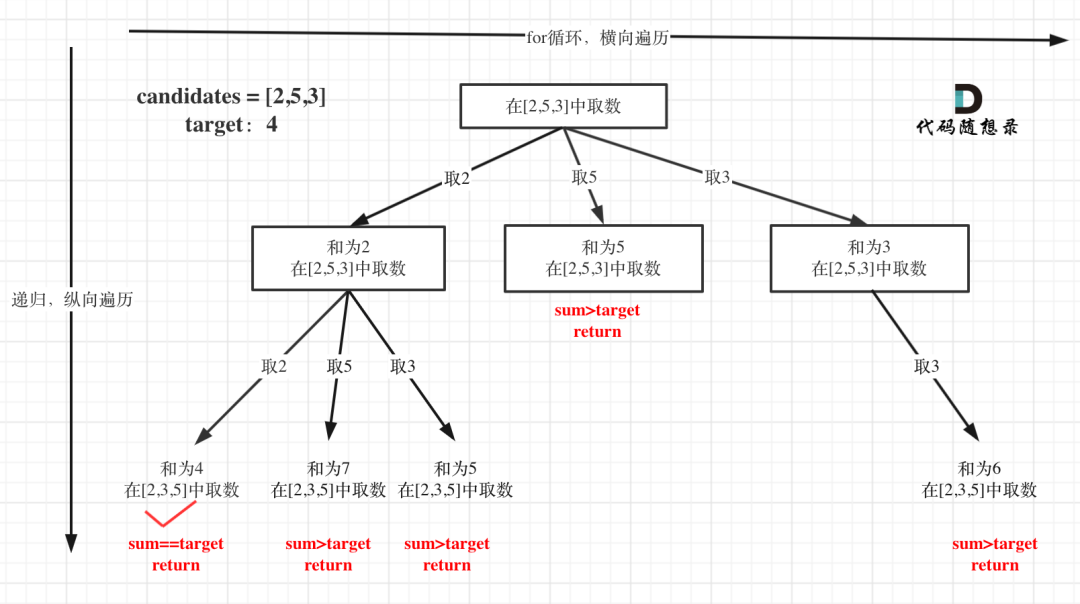
代码
1 class Solution { 2 public: 3 vector<int>path; 4 vector<vector<int>> res; 5 void backtracking(const vector<int>& candidates,int target,int sum,int startIndex){ 6 if(sum > target){ 7 return; 8 } 9 if(sum == target){ 10 res.push_back(path); 11 return; 12 } 13 for(int i = startIndex;i < candidates.size();i++){ 14 sum += candidates[i]; 15 path.push_back(candidates[i]); 16 backtracking(candidates,target,sum,i); 17 sum -= candidates[i]; 18 path.pop_back(); 19 } 20 } 21 vector<vector<int>> combinationSum(vector<int>& candidates, int target) { 22 backtracking(candidates,target,0,0); 23 return res; 24 } 25 };
再进行剪枝优化
上面代码可知,我们是在 sum > target 时,结束递归,实际上在上一次递归尾部就可进行预判,也就是不用进入这层递归,即如果知道下层递归 sum > target 那么就没有必要进入下一层递归了。
如何进行修改呢 ?我们可以增强进入 for 循环的条件,因为只要进入了 for 循环,就会进入下一层递归。对总集合排序之后,如果下一层的sum(就是本层的 sum + candidates[i])已经大于target,就可以结束本轮for循环的遍历。
for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++)

1 class Solution { 2 public: 3 vector<int>path; 4 vector<vector<int>> res; 5 void backtracking(const vector<int>& candidates,int target,int sum,int startIndex){ 6 if(sum > target){ 7 return; 8 } 9 if(sum == target){ 10 res.push_back(path); 11 return; 12 } 13 for(int i = startIndex;i < candidates.size() && sum + candidates[i] <= target;i++){ 14 sum += candidates[i]; 15 path.push_back(candidates[i]); 16 backtracking(candidates,target,sum,i); 17 sum -= candidates[i]; 18 path.pop_back(); 19 } 20 } 21 vector<vector<int>> combinationSum(vector<int>& candidates, int target) { 22 sort(candidates.begin(),candidates.end()); 23 backtracking(candidates,target,0,0); 24 return res; 25 } 26 };
一定要先进行排序,再去回溯