最短编辑距离

题目

分析

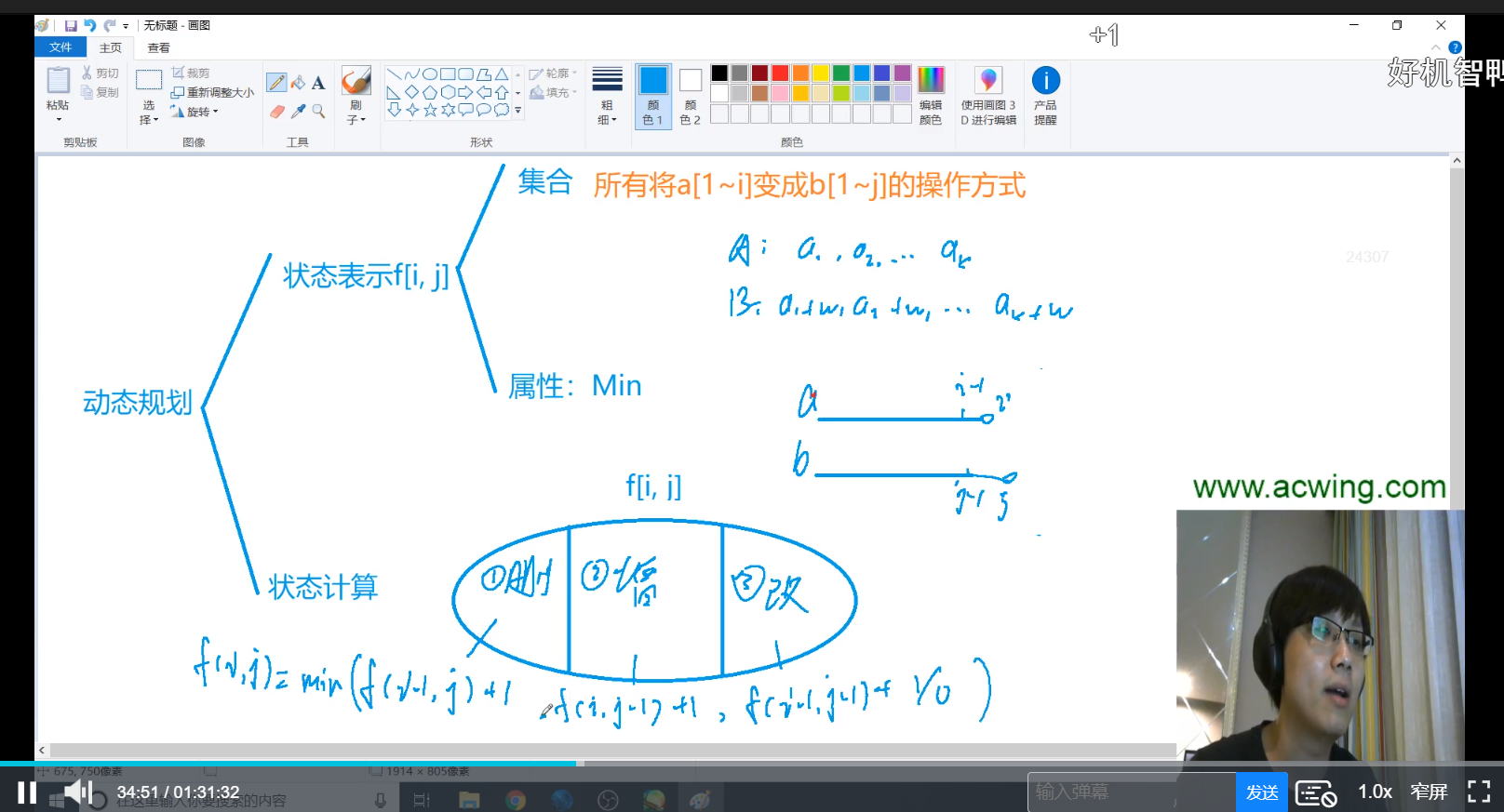
根据最长公共子序列中状态表示的技巧，本题依旧两个串。状态标识设 dp[i,j] 表示将a[1-i] 变为 b[1-j] 的所有操作方式的集合中最少操作次数。

其实做了几道线性dp的题目，发现还是有些技巧：就是大都根据最后一个状态或者最后一个或一对元素考虑

递推公式的推导：考虑元素a[i] 和 b[j]的三种操作

1. 通过删除a[i] 使得 a[1-i] 变为 b[1-j]，意味着a[1-i-1]与b[1-j]已经匹配 。

　　dp[i,j] = dp[i-1,j]  + 1

2. 通过对a数组增加元素使得  a[1-i+1] 变为 b[1-j]，意味着a[1-i]与b[1-j-1]已经匹配 

　　dp[i,j] = dp[i,j-1]  + 1

3.通过修改a[i]使得  a[1-i] 变为 b[1-j]，意味着[1-i-1]与b[1-j-1]已经匹配 

　　dp[i,j] = dp[i,j-1]  + (1/0)       若a[i] == b[j] 则不用加1，若不等则需要改a[i]，加1

最终 dp[i][j] = min(dp[i-1,j]  + 1, dp[i,j-1]  + 1,dp[i,j-1]  + (1/0)   

代码

#include<iostream>
#include<algorithm>
#include<climits>
using namespace std;

const int N = 1010;
char a[N],b[N];
int dp[N][N];
int main(){
    int n,m;
    scanf("%d%s",&n,a+1);
    scanf("%d%s",&m,b+1);
    //边界初始化 
    //若a数组0个元素，则a只能添加操作
    for(int i = 0;i <= m;i++) dp[0][i] = i;
    //若b数组0个元素，则a只能删除操作
    for(int i = 0;i <= n;i++) dp[i][0] = i;
    
    for(int i = 1;i <= n;i++){
        for(int j = 1;j <= m;j++){
            dp[i][j] = min(dp[i-1][j],dp[i][j-1]) + 1;
            if(a[i] == b[j]){
                dp[i][j] = min(dp[i][j],dp[i-1][j-1]);
            }
            else{
                dp[i][j] = min(dp[i][j],dp[i-1][j-1]+1);
            }
                
        }
    }
    printf("%d",dp[n][m]);
    return 0;
}

注意边界条件！！！第0行或第0列并不一定全为0！！！

时间复杂度O(N²)