经典题目4 VOJ1049
题目大意:顺次给出m个置换,反复使用这m个置换对初始序列进行操作,问k次置换后的序列。m<=10, k<2^31。
首先将这m个置换“合并”起来(算出这m个置换的乘积),然后接下来我们需要执行这个置换k/m次(取整,若有余数则剩下几步模拟即可)。注意任意一个置换都可以表示成矩阵的形式。例如,将1 2 3 4置换为3 1 2 4,相当于下面的矩阵乘法:

置换k/m次就相当于在前面乘以k/m个这样的矩阵。我们可以二分计算出该矩阵的k/m次方,再乘以初始序列即可。做出来了别忙着高兴,得意之时就是你灭亡之日,别忘了最后可能还有几个置换需要模拟。
注意:这m个置换对应的矩阵相乘的时候必须左乘
代码如下:

1 #include<stdio.h> 2 #include<string.h> 3 #define N 110 4 struct Matrix 5 { 6 int a[N][N]; 7 }origin,res,tmp,A,B,ans; 8 int n; 9 int op[N][N]; 10 Matrix mul(Matrix x,Matrix y) 11 { 12 int i,j,k; 13 memset(tmp.a,0,sizeof(tmp.a)); 14 for(i=1;i<=n;i++) 15 for(j=1;j<=n;j++) 16 for(k=1;k<=n;k++) 17 tmp.a[i][j]+=x.a[i][k]*y.a[k][j]; 18 return tmp; 19 } 20 Matrix quickpow(Matrix B,int k) 21 { 22 int i; 23 memset(res.a,0,sizeof(res.a)); 24 for(i=1;i<=n;i++) 25 res.a[i][i]=1; 26 while(k) 27 { 28 if(k&1) 29 res=mul(res,B); 30 B=mul(B,B); 31 k>>=1; 32 } 33 return res; 34 } 35 void print(Matrix B) 36 { 37 int i,j; 38 for(i=1;i<=n;i++) 39 { 40 for(j=1;j<=n;j++) 41 printf("%d ",B.a[i][j]); 42 printf("\n"); 43 } 44 printf("+++++++++\n"); 45 } 46 int main() 47 { 48 int m,i,k,j; 49 while(scanf("%d%d%d",&n,&m,&k)!=EOF) 50 { 51 memset(B.a,0,sizeof(B.a)); 52 for(i=1;i<=n;i++) 53 B.a[i][i]=1; 54 for(i=1;i<=m;i++) 55 { 56 for(j=1;j<=n;j++) 57 scanf("%d",&op[i][j]); 58 memset(A.a,0,sizeof(A.a)); //置换所对应的矩阵 59 for(j=1;j<=n;j++) 60 A.a[j][op[i][j]]=1; 61 B=mul(A,B); //左乘 62 // print(B); 63 } 64 res=quickpow(B,k/m); //执行k/m次 65 memset(origin.a,0,sizeof(origin.a)); 66 for(i=1;i<=n;i++) 67 origin.a[i][1]=i; 68 ans=mul(res,origin); //乘以初始矩阵 69 if(k%m) //将剩余的几步模拟 70 { 71 for(i=1;i<=k%m;i++) 72 { 73 memset(A.a,0,sizeof(A.a)); 74 for(j=1;j<=n;j++) 75 A.a[j][op[i][j]]=1; 76 ans=mul(A,ans); 77 } 78 } 79 for(i=1;i<=n;i++) 80 { 81 printf("%d",ans.a[i][1]); 82 if(i<n) 83 printf(" "); 84 } 85 printf("\n"); 86 } 87 return 0; 88 }
hdu 2371 Decode the Strings
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=2371
题目大意:给出n 和m,给出n个数,代表一个置换,接着一个字符串s,s经过m次置换后变成另一个字符串,
现在给出经过m次置换后的字符串,输出原始字符串s
比如:5 3
2 3 1 5 4
hello
需经过3次置换,则"hello" -> "elhol" -> "lhelo" -> "helol"
思路:将置换规则取反(将p[i]位置上的数num[i]变成p[num[i]]上的数,例如,num: 2 3 1 5 4 变成 num: 3 1 2 5 4
p: 1 2 3 4 5 p: 1 2 3 4 5 )
然后将m次置换合并起来,即算出这m个置换的乘积(即origin^m),然后乘以初始序列[1 2 3 4 ....n],然后输出对应位置的字符即可。
注意任意一个置换都可以表示成矩阵的形式。例如,将1 2 3 4置换为3 1 2 4,相当于下面的矩阵乘法:
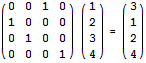
m次置换就相当于前面乘以m个这样的矩阵,用矩阵快速幂即可。
代码如下:

1 #include<stdio.h> 2 #include<string.h> 3 #define N 100 4 struct Matrix 5 { 6 int a[N][N]; 7 }res,tmp,origin,A,ans; 8 int n; 9 int p[N],num[N]; 10 char s[N]; 11 Matrix mul(Matrix x,Matrix y) 12 { 13 int i,j,k; 14 memset(tmp.a,0,sizeof(tmp.a)); 15 for(i=1;i<=n;i++) 16 for(j=1;j<=n;j++) 17 for(k=1;k<=n;k++) 18 tmp.a[i][j]+=x.a[i][k]*y.a[k][j]; 19 return tmp; 20 } 21 void quickpow(int k) //矩阵快速幂 22 { 23 int i; 24 memset(res.a,0,sizeof(res.a)); 25 for(i=1;i<=n;i++) 26 res.a[i][i]=1; 27 while(k) 28 { 29 if(k&1) 30 res=mul(res,origin); 31 origin=mul(origin,origin); 32 k>>=1; 33 } 34 } 35 36 int main() 37 { 38 int m,i; 39 while(scanf("%d%d",&n,&m)!=EOF) 40 { 41 if(n==0&&m==0) 42 break; 43 for(i=1;i<=n;i++) 44 scanf("%d",&num[i]); 45 for(i=1;i<=n;i++) //将置换取反 46 p[num[i]]=i; 47 memset(origin.a,0,sizeof(origin.a)); //将置换用矩阵表示 48 for(i=1;i<=n;i++) 49 origin.a[i][p[i]]=1; 50 getchar(); 51 gets(s); 52 quickpow(m); //乘以m次这样的矩阵 53 memset(A.a,0,sizeof(A.a)); //原始序列[1 2 3 4 5 ...n] 54 for(i=1;i<=n;i++) 55 A.a[i][1]=i; 56 ans=mul(res,A); //与原始序列相乘 57 for(i=1;i<=n;i++) 58 printf("%c",s[ans.a[i][1]-1]); 59 // printf("%d ",ans.a[i][1]); 60 printf("\n"); 61 } 62 return 0; 63 }
