【什么是RAID】
RAID的概念描述在互联网上比比皆是,用最简单的原理描述,就是在定义存储方式时允许在一部分数据缺失的情况下不影响全部数据,类似于通讯领域的纠错码。不同的冗余模式形成了不同的RAID类别。
【单一冗余模型】
我们需要先描述仅具备一个磁盘冗余的RAID模型(思想同RAID3,RAID4,RAID5)。假设现在有3页空白的纸,用来记录一些数字,为了更清晰地记录,我们先将每页白纸划出相同大小的一些表格。再假设有一个可能:这3页纸,特定情况下会有其中某一页丢失。为了在上述设定情况保证这些数字能完整安全的记录下来,我们要设计一些互相牵连的冗余关系。如我们要记录的数字序列是:3、14、28、4、98、88 。我们可以依次在第1页和第2页写要记录的数字,在第3页写上他们的和。如下图所示:
根据上图,可以很容易的分析出,不管这3页中的哪一页丢失,都可以通过另两页计算另一页的数据来。很显然,即使是超过3页的情况,按上述方式设计记录模式,也可以支持任意一页记录的丢失。但这个模型却不会在实际中应用,原因来自于上图的第三行数据:98+88 = 186 ,从这行的运算来看,为了记录整个一行数据的和,校验页所用的空间要大于等于任何一个数据页。其实,校验和的总容量要等于所有数据页的总容量,换个角度说,如果记录的是10页数据,那么可能要用另外10页的空间来记录校验,这是完全没有意义的方案(与其这样,还不如所有数据抄两份,即RAID1的模型)。所以,一些工程师开始用别的算法代替加法,以减少校验和的总容量,但算法的实现效果需要与加法完全相同,同时运算要足够简单。最好的方案就是异或。异或是基于位的运算,首先其运算性能非常好,无需更多的专门运算器。同时异或算法完全满足正运算与逆运算的完全映射(即,正运算的结果唯一,同时这个正运算的逆运算结果也唯一。这个在数学上叫什么?恕笔者数学底子差,暂时这样称呼),满足交换律和结合律。而且最重要的是,异或不会升位。用异或算法改写后的存储记录如下:
可以很清晰得看到,第三行的校验和,不再是3个数字,而且不论多少个数据成员,用异或得到的校验和容量不会累加。为了更好的概括,我们用"+"表示这个正向的校验运算,用“-”表示其逆运算。在我们最初的描述中,就表示数字的加减法,之后"+"表示异或,“-”也是异或(异或的逆运算也是异或,所以运算器简单,速度快)。假设有n个存储成员,把每个存储成员划分成若干个存储单元,其中n-1(数学减法,下面的Dn-1同理)个成员盘为数据,1个成员盘为校验。每个水平条带上的校验关系如下:
D1 + D2 + D3 + ... +Dn-1 = P1
Dx = P1 - D1 - D2 - D3 - ... -Dn-1(D序列中排除Dx)
也就是:Dx = P1 + D1 + D2 + D3 +... +Dn-1(D序列中排除Dx)
【多次冗余模型】
上述单一冗余仅支持一个存储成员的缺失,在实际中有可能需要更高的冗余性,则需要更进一步对算法进行改进。如果需要设计一种存储模型,实现在缺失2个成员的情况下,存储整体依然可以运算完整,最好的数学模型恐怕就是二元一次方程了,形如下面方程组:
aX+bY=c
dX+eY=f。 其中a/d != b/e
上述方程式用到乘法与除法,同时,乘法与除法完全可逆,且满足交换律、结合律与分配率。还是在加法中遇到的困难,普通的数学乘法会导致校验容量的累加,所以不可取。有没有一种乘除法符合我们的要求呢?有!---基于伽罗华域的乘除法。数学概念是很抽象的,仅以GF(2^8)为例,我们设计一个有限循环域,域上仅有0-255这几个数字,这些数字之间再设计一个完整的加减乘除运算,其结果依然在这些数字中,而且运算结果唯一,无二义性。我们来设计一种算法,对于2,如果2的n次方大于某个值(本原多项式),则让其对这个值(本原多项式)取余,确保又折回到0-255这个范围内,如果从2^0,2^1,2^2,,,直到2^255,按这个规律做运算,得到的值均处于0-255范围内,且均不相等,这样就形成了一个一对一的映射关系,同时满足2的这些次幂与结果之间就乘法/除法的运算规律(具体理论需参考群、环、域、有限域等数学理论)。在GF(2^8)上,有16个满足条件的本原多项式,分别如下:
1 x8+x7+x6+x5+x4+x2+1 1 1111 0101 = 0x1F5
2 x8+x7+x6+x5+x2+x+1 1 1110 0111 = 0x1E7
3 x8+x7+x6+x3+x2+x+1 1 1100 1111 = 0x1CF
4 x8+x7+x6+x+1 1 1100 0011 = 0x1C3
5 x8+x7+x5+x3+1 1 1010 1001 = 0x1A9
6 x8+x7+x3+x2+1 1 1000 1101 = 0x18D
7 x8+x7+x2+x+1 1 1000 0111 = 0x187
8 x8+x6+x5+x4+1 1 0111 0001 = 0x171
9 x8+x6+x5+x3+1 1 0110 1001 = 0x169
10 x8+x6+x5+x2+1 1 0110 0101 = 0x165
11 x8+x6+x5+x+1 1 0110 0011 = 0x163
12 x8+x6+x4+x3+x2+x+1 1 0101 1111 = 0x15F
13 x8+x6+x3+x2+1 1 0100 1101 = 0x14D
14 x8+x5+x3+x2+1 1 0010 1101 = 0x12D
15 x8+x5+x3+x+1 1 0010 1011 = 0x12B
16 x8+x4+x3+x2+1 1 0001 1101 = 0x11D
常用0x11D做为raid6的本原多项式,意思是2的n次方如果大于0x11D,就对于做xor的取余运算,确保结果小于0x256,这样就可以算出2^0到2^255之间的所有数值。GF(2^8)上的加减法同样是异或算法(xor)。GF(2^8)上的乘法即多项式乘法,但依然要对本原多项式取xor余,在算法设计上,有多种计算方式,但在GF(2^8)上,最快的推荐方法是查表法,只需事先计算好所有的0~255 分别乘以 0~255的值,生成65536个值的表格,计算时直接查表即可。也有使用对数查表法,使乘法转变为加法进行运算的,需要查表和加法结合使用。GF(2^8)上的除法可转换为对其逆元的乘法,即a 除以 d,假设d对应于(x的m次幂),那找出对应(x的255-m次幂)的值d',a除以d,即等于a乘以d'。
【RAID6】
在加减乘除都确定后,2元一次方程组就可以求解了。所以,一个以此原理生成的RAID的结构设计大致如下图(以5块盘为例,P为第一重校验,Q为第二重校验,xn为数据):
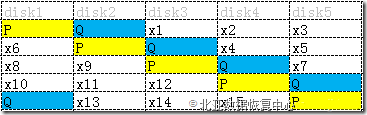
之所以P和Q螺旋式循环分布,是为了使所有磁盘负载均衡,如果不好理解,可以把P和Q单独放在一列中,算法的意义是相同的。再重复一下,下面提及的+、-、*、/运算都是指基于GF(2^8)上的加、减、乘、除。P值等于同一行(条带)上的所有单元相加的和。或者可以理解为1与每个单元相乘后的累加和,如第一个条带的P:
P= x1+x2+x3 也就是P=1*x1 + 1*x2 + 1*x3
在GF(2^8)上,每个多项式对应一个0~255的值,即d0对应多项式X的0次幂,d1对应多项式X的2次幂等,按多项式展开,X为2进制,故d0 = 1,d1 =2,d2=4 ,d3=8,等等,如下表所示:

返回RAID结构图中,Q值等于每个数值单元格乘以他们的相应的dn再累加的结果,其中dn可约定,只需保证同一条带的运算中不重复出现dn即可,如第一行的Q可以为:
Q = d1* x1 + d2*x2 +d3*x3
这样,对于每一行(条带),就可以保证任意2个单元丢失,都可以计算出来(为了明了,以下计算直接将减法改为加法):
以第一行为例:
a) 如果P,Q均丢失,数据区不影响,x1,x2,x3均可正常读写
b)如果xn丢失,根据P或Q都可计算出来(实际中,因P 的计算更快速,通常会使用P校验计算出丢失的 xn)
c)如果P,xn丢失,P值不做处理,假设丢失的是x2,根据Q值的定义
Q = d1* x1 + d2*x2 +d3*x3
=> d2*x2 = Q + d1*x1 + d3*x3
=> x2 = (Q + d1*x1 + d3*x3) * x253 ;//注:x253为x2的逆元,可以查表得到
d) 如果两个x丢失,则可根据二元一次方式的标准解法进行求解,假设丢失的是x1,x3:
P = x1+x2+x3
Q = d1* x1 + d2*x2 +d3*x3
=> x1 = P + x2 + x3
=> Q = d1 * (P + x2 + x3) +d2*x2 +d3*x3
=> Q = d1*P + d1*x2 + d1* x3 + d2*x2 + d3*x3
=> Q = d1*P + d1*x2 + d2*x2 + d1*x3 + d3*x3
=> Q + d1*P + d1*x2 + d2*x2 = (d1+d3) * x3
=> x3 = ( Q + d1*P + d1*x2 + d2*x2) / (d1+d3)
查表法得到(d1 + d3)的逆元dn后,可知
x3 = ( Q + d1*P + d1*x2 + d2*x2) * dn
再根据P= x1 + x2 + x3求得x1,即完成所有数据的补缺。
本文出自 “张宇(数据恢复)” 博客,请务必保留此出处http://zhangyu.blog.51cto.com/197148/1134820