正则化（Regularization）

我们在使用线性回归和逻辑斯特回归的时候，高次幂的多项式项可能造成过拟合的问题。而我们使用过拟合这一方法来改善或者减少这一问题。

我们所要做的就是使θ尽可能接近0，那么对于高阶项对于h_θ(x)的影响也会尽量小，几乎没有。这样就预防了过拟合。

正则化的线性回归模型

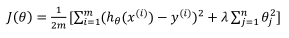
是正则项，λ是正则化参数，λ的作用是控制两个目标之间的取舍，即更好地拟合训练集的目标和将参数控制得更小的目标，从而保持假设模型的相对简单避免出现过拟合的现象。所以对于λ的值应当慎重选择。

既然我们加入了正则项，那么我们在梯度下降的时候也是要做出一点改变，将梯度下降算法分为两种情形

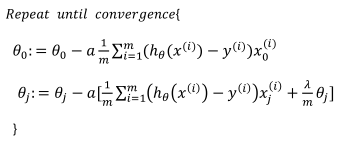
对于上面的算法中j=1,2，……，n时的更新石子进行调整可得：

可以看出，正则化线性回归的梯度洗将算法的变化在于，每次都在原有算法更新规则的基础上令θ值减少了一个额外的值。

线性回归正则方程式正则化

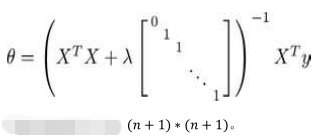
正则化的逻辑斯特回归模型

要最小化该代价函数，通过求导，得出梯度下降算法为：

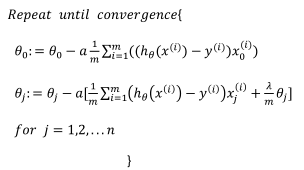
最后附上正则化的逻辑斯特回归模型的python代码实现

import numpy as np
def costReg(theta,X,y,learningRate):
    theta=np.matrix(theta)
    X=np.matrix(X)
    y=np.matrix(y)
    first=np.multiply(-y,np.log(sigmoid(X*theta.T)))
    second=np.multiply((1-y),np.log(1-sigmoid(X*theta.T)))#multiply数组和矩阵对应位置相乘，输出与相乘数组/矩阵的大小一致
    reg=(learningRate/(2*len(X))*np.sum(np.power(theta[:,1:theta.shape[1]],2)))#thate.shape[1]指thate矩阵的第一维
    return np.sum(first-second)/len(X)+reg