神经网络学习1

神经网络模型建立在很多神经元之上，每个神经元又是一个学习模型。这些蛇恩静元也叫作激活单元。下面我们以一个逻辑斯特回归模型作为自身学习模型，参数又可以被称为权重。

其中x₁，x₂，x₃是输入单元，我们将原始数据输入给它们。a_1，a₂，a₃是中间单元，它们负责将数据进行处理，然后呈递到下一层。最后是输出单元，它负责计算h_θ(x)。如上图所示，第一层为输入错，最后一次为输出层，中间一层为隐藏层。我们的每一层其实都有一个偏差单位，相当于x0，其值始终为1。

代表第j层的第i个激活单元。θ⁽ⁱ⁾权重矩阵它控制从某一层到某一层的映射。θ⁽ⁱ⁾的维度是3*4。

对于上图所示的模型，激活单元和输出分别表达为：

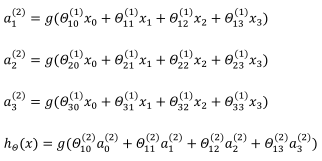
在这里a⁽¹⁾=x=     z⁽²⁾=

加上偏置单元x₀=1对a⁽²⁾并无影响。

接下来我们拟合神经网络的代价参数

假设我们要区分出K个类，那么K个类有K个输出单元(K>-3)

(h_θ(x))_i=第i个输出

 那么我们的代价函数就为

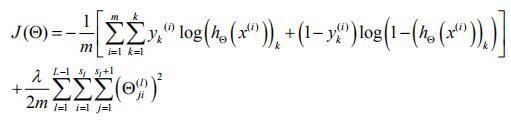
我们现在设δ为误差，δ上面的参数为(l)下面的参数是j，表示第l层的第j个输出项和y之间的误差。

假如我们现在又一个4层的训练集，按照向前传播算法可以得到下图所示算式。

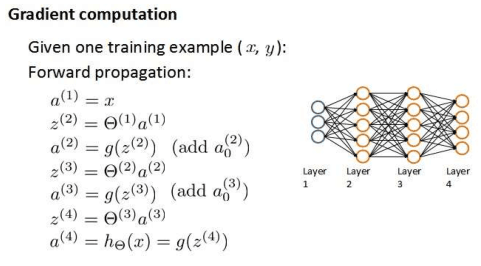
我们现在使用向后传播算法来计算误差δ。

则δ⁽⁴⁾=a⁽⁴⁾-y

我们利用这个误差来计算前一层的误差：,g‘（z⁽³⁾)=a⁽³⁾_*(1-a⁽³⁾)。而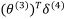则是权重导致的误差的和。然后可以依次类推之后的误差。而第一层是输入变量，不存在误差。

当我们有了所有的表达式后，就可以计算代价函数的偏导数了，假设λ=0，即我们不做任何正则化处理时有：

在上面这个式子里，它的下标分别代表着下面这几种意思：

l代表目前所计算的是第几层。

j代表目前计算层

中的激活单元的下标，也将是下一层的第j个输入变量的下标。

i代表下一层中误差单元的下标，是受到权重矩阵中第i行影响的下一层中的误差单元的下标。

如果我们考虑正则化处理，并且我们的训练集是一个矩阵而不是向量，在上面的特殊情况中，我们需要计算每一层的误差单元来计算代价函数的偏导数。在更为一般的情况中，我们同样需要计算每一层的误差单元，但是我们需要为整个训练集计算误差单元，此时的误差单元也是一个矩阵，我们用大写的δ来表示这个误差矩阵。我们计算大写δ的算法表示为：

 

即首先用整向传播方法计算出每一层的激活单元，利用训练集的结果与神经网络预测的结果求出最后一层的误差，然后利用该误差运用反向传播法求取直至第二层的所有误差。

那么我们一般情况下的偏导数的计算方法如下：