基本概念
序列密码的加密用一个随机序列(密钥流)与明文序列按位叠加产生密文,用同一随机序列与密文序列叠加来恢复明文。
v由种子密钥通过密钥流发生器得到的密钥流为:(K=k_1k_2...k_n),则加密变换为:(C=c_1c_2...c_n)
其中(c_i=m_i⊕k_i;i=1,2...n),那么解密变换就是(m_i=c_i⊕k_i;i=1,2...n)
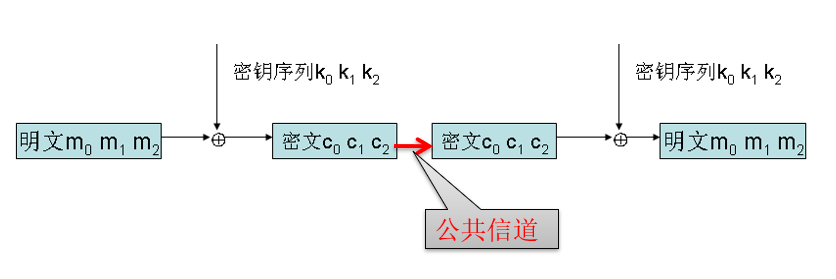
密码强度主要依赖于密钥流的安全性
同步序列密码
密钥序列的产生独立于明文消息和密文消息。
特点:
- 无错误传播:各符号之间真正独立。一个传播错误只影响一个符号,不会影响到后继的符号
- 同步:发送方和接收方必须保持精确的、用同样的密钥并作用在同样的位置上,才能正确的解密
自同步序列密码
密钥序列是密钥及固定大小的以往密文的函数,依赖于密文。
特点:
- 有限错误传播:设密钥序列产生器具有n位存储,则一个符号的传输错误只影响到后面n符号的解密
- 自同步:只要接收方连续收到n个正确的密文符号,密钥序列产生器便会自动地恢复同步
- 消除明文统计特性
密钥流生成器和密钥流
密钥流的要求
- 极大的周期:随机序列是非周期的,而按任何算法产生的序列都是周期的,因此应要求密钥流具有尽可能大的周期
- 良好的统计特性:随机序列有均匀的游程分布
游程:指序列中相同符号的连续段,其前后均为异种符号。
例如:……0 111 0000 10……
注意:计算游程的时候要首尾相连计算,头和尾的两个0合在一起构成长度为2的0游程。
有长为3的1游程、长为4的0游程、长为1的1游程,长为2的0游程。一般要求其在周期内满足:同样长度的0游程和1游程的个数相等,或近似相等。
- 很高的线性复杂度:不能用级数较小的线性移位寄存器LFSR近似代替
- 用统计方法由密钥序列(k_0k_1k_2…ki…)提取密钥生成器结构或种子密钥在计算上不可行
密钥流生成器
密钥流生成器可以分为:
- 驱动部分
- 非线性组合部分
驱动部分:控制生成器的状态序列,为非线性组合部分提供统计性能良好的序列
-
周期很大
-
分布较随机
非线性部分:将驱动部分提供的序列组合成密码特性好的序列
- 可隐蔽驱动序列与密钥k之间明显的依赖关系
目前密钥流生成器大都基于移位寄存器FSR
通常由线性移位寄存器(LFSR)和一个非线性组合函数即布尔函数组合,构成一个密钥流生成器
(a)由一个线性移位寄存器和一个滤波器构成
(b)由多个线性移位寄存器和一个组合器构成
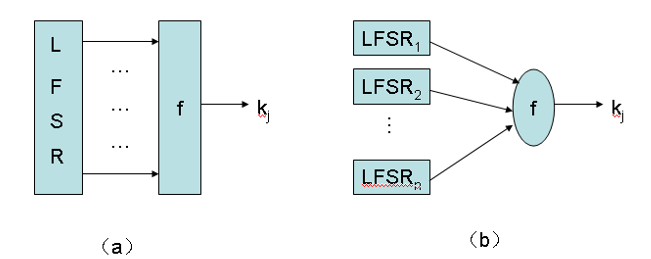
LSFR的优点:
- 非常适合硬件实现
- 能产生大的周期序列
- 能产生统计特性好的序列
- 能够应用代数方法进行很好的分析
反馈移位寄存器
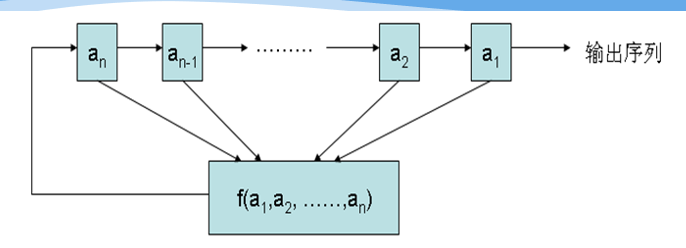
GF(2)上一个n级反馈移位寄存器由n个二元存储器与一个反馈函数(f(a_1a_2 ... a_n))组成
-
每个存储器称为移位寄存器的一级
-
在任一时刻,这些级的内容构成该FSR的状态;对应于一个GF(2)上的n维向量,共有(2^n)种可能的状态
-
状态可用n长序列(a_1, a_2, a_3, …, a_n)或n维行向量((a_1, a_2, a_3, …, a_n))表示
-
每一级存储器(a_i)将其内容向下一级(a_{i-1})传递,并根据存储器当前状态计算(f(a_1, a_2, a_3, …, a_n))作为(a_n)下一时间的内容
example:
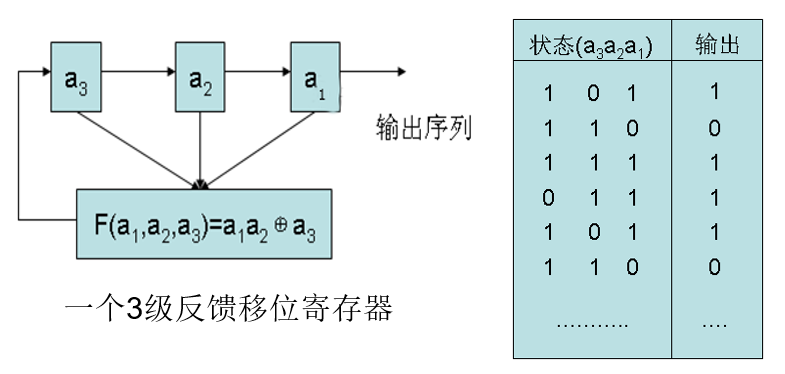
初始状态为((a_1,a_2,a_3)=(1,0,1)),输出可由上表求出,其输出序列为(10111011101…),周期为4
如果反馈函数(f(a_1, a_2, …, a_n))是(a_1, a_2, …, a_n)的线性函数,则称为线性反馈移位寄存器(LFSR)
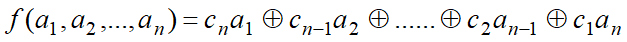
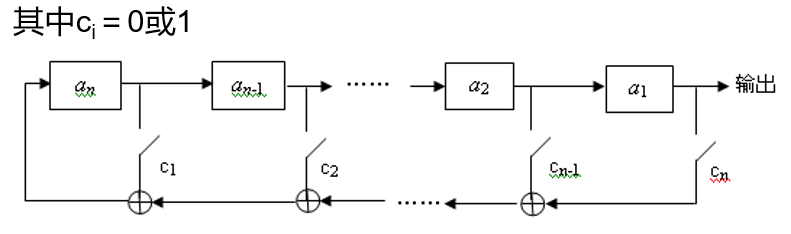
n级LFSR最多有(2^n)个不同的状态
初始状态为零,则其状态恒为零
若其初始状态非0,则其后继状态不会为0
因此n级LFSR的状态周期(≤2^n-1)
输出序列的周期与状态周期相等,所以$≤2^n-1 $
选择合适反馈函数可使序列周期达到最大值(2^n -1),周期达到最大值的序列称为m序列
特征多项式表示:
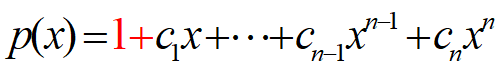
1是必须写的,(c_i)的取值和上面一一对应
定理:n级LFSR产生的序列有最大周期(2^n-1)的必要条件是其特征多项式为不可约的
定义:若n次不可约多项式(p(x))的阶为(2^n-1),则称(p(x))是n次本原多项式,使得(p(x)|(x^p-1))的最小p称为(p(x))的阶
定理:设({a_i}∈G(p(x))),({a_i})为m序列的充要条件是(p(x))为本原多项式
Java实现LSFR
public class LSFR {
public static void newLsfr(List<Integer> lst, int k, List<Integer> key){
int temp=0;
List<Integer> temp1 = new ArrayList<>(lst);
List<Integer> temp2 = new ArrayList<>(key);
for(int i = 0;i < k; ++i){
boolean flag = false;
Integer kOut=0;
for (int j = 0;j < 20;++j){
if(temp2.get(j).equals(1))
kOut = (Integer) ((kOut + temp1.get(j) ^ temp2.get(j)) % 2);
}
temp1.remove(0);
temp1.add(kOut);
for(int q = 0;q < 20;q++){
if (!temp1.get(q).equals(lst.get(q))) {
flag = true;
break;
}
}
System.out.println(temp1.toString()+"第"+(i+1)+"次");
if(!flag)
temp = i+1;
}
if(temp!=0)
System.out.println("周期是:"+temp);
}
对于m-序列(周期为(2^n-1)),如果攻击者知道了(2n)位明密文对,则可确定反馈多项式的系数,从而确定该LFSR接下来的状态,也就能得到余下的密钥序列,具体过程如下:


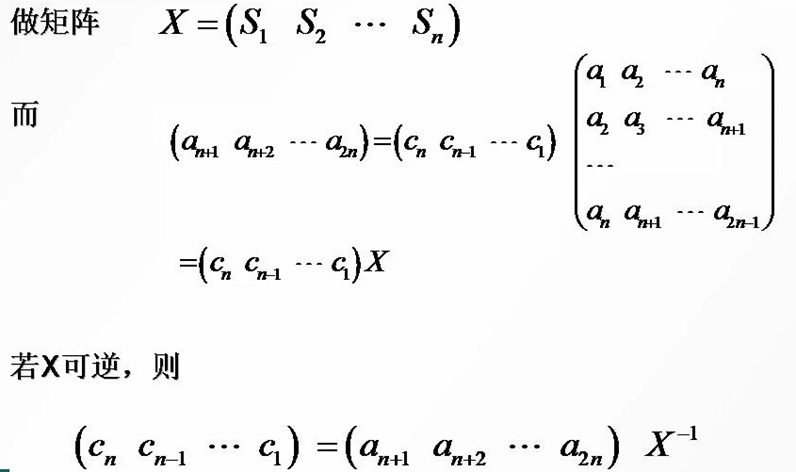
三个随机性公设:
在一个周期内,0与1的个数相差至多为1—({a_i})中0与1出现的概率基本上相同
在一个周期内,长为1的游程占游程总数的(1/2),长为2的游程占游程总数的(1/2^2),……,长为(i)的游程占游程总数的(1/2^i),……,且等长的游程中0游程个数和1游程个数相等——0与1在序列中每一位置上出现的概率相同
异相自相关函数是一个常数——通过对序列与其平移后的序列做比较,不能给出其它任何信息
非线性部分
- Geffe发生器
- 钟控发生器
- 交错停走式发生器
- 门限发生器
常用流密码算法
- RC4
基于非线性数组变换
优点:易于软件实现,加密解密速度快,比DES快10倍
- A5
基于LFSR