地形部分的原理介绍的差不多了,但之前还有一个刻意忽略的地方,就是地形的重采样。通俗的讲,如果当前Tile没有地形数据的话,则会从他父类的地形数据中取它所对应的四分之一的地形数据。打个比方,当我们快速缩放影像的时候,下一级的影像还没来得及更新,所以会暂时把当前Level的影像数据放大显示, 一旦对应的影像数据下载到当前客户端后再更新成精细的数据。Cesium中对地形也采用了这样的思路。下面我们具体介绍其中的详细内容。
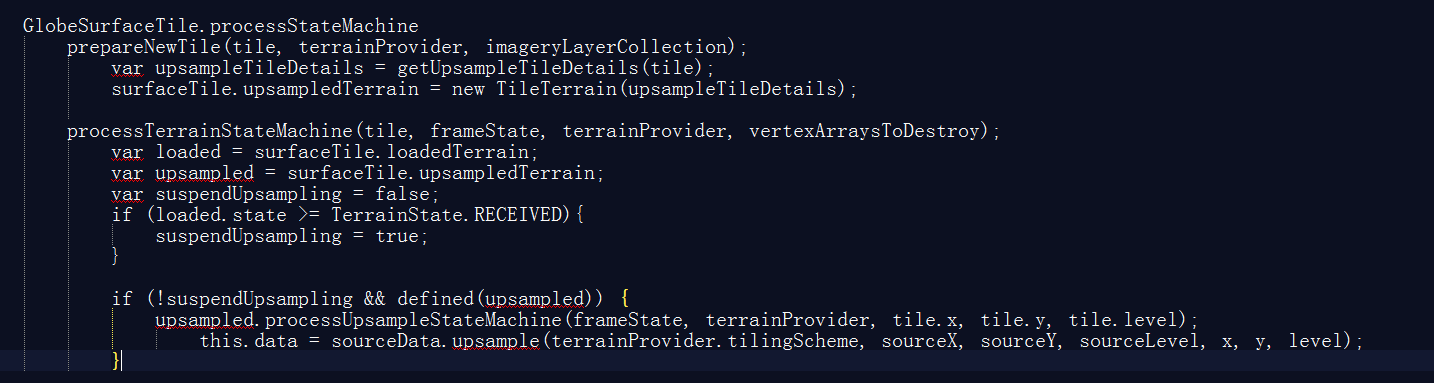
上图是一个大概流程,在创建Tile的时候(prepareNewTile),第一时间会获取该Tile父节点的地形数据(upsampleTileDetails),然后构造出upsampledTerrain对象,它是TileTerrain对象,只是一个包含父类地形信息的空壳。接着,开始创建地形网格(processTerrainStateMachine)。
这里就有两个逻辑,如果当前没有地形数据,也就是EllipsoidTerrainProvider的情况,这样会直接创建HeightmapTerrainData。因此状态是TerrainState.RECEIVED,这种情况下不需要重采样;如果请求了真实的地形数据,比如CesiumTerrainProvider,无论是请求高度图还是STK,只要有异步请求,则会执行processUpsampleStateMachine韩式,最终实现重采样(sourceData.upsample)。
HeightmapTerrainData.prototype.upsample
我们先了解一下高度图下的实现。高度图,顾名思义也是一种图了,所以这个重采样的方式和普通的图片拉伸算法一致。比如一个2*2的图片,放大至4*4的大小,这里就有一个插值的过程。比如线性差值,会取相邻的两个像素颜色,加权求值,或者双线性插值,取周边四个像素,加权求值。这让我想到了GDI中对图片是采用线性了,而Photoshop里面则有很多专业的选项,某些逗逼用户经常拿着PS拉伸的效果来做对比,说我们图片拉伸的效果不如PS。等我们做完了,又拿CorelDraw来对比矢量效果。但你有很难从技术和产品的角度来和用户沟通其中的利弊。这是题外话了,我们来看一下Cesium具体的代码:
for (var j = 0; j < height; ++j) { var latitude = CesiumMath.lerp(destinationRectangle.north, destinationRectangle.south, j / (height - 1)); for (var i = 0; i < width; ++i) { var longitude = CesiumMath.lerp(destinationRectangle.west, destinationRectangle.east, i / (width - 1)); var heightSample = interpolateMeshHeight(buffer, encoding, heightOffset, heightScale, skirtHeight, sourceRectangle, width, height, longitude, latitude, exaggeration); setHeight(heights, elementsPerHeight, elementMultiplier, divisor, stride, isBigEndian, j * width + i, heightSample); } }
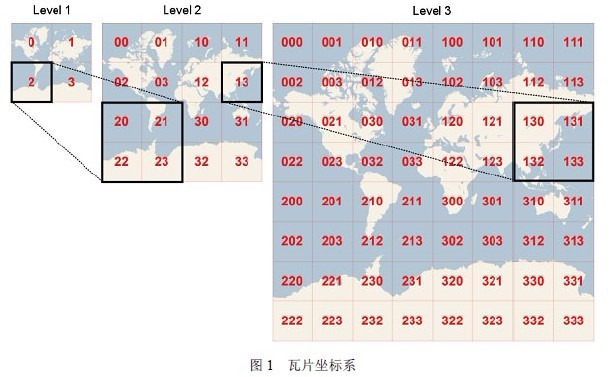
这是两个for循环,遍历目标图片中每一个经纬度对应父类图片中该位置的高度值。下面是一个切片四叉树的示意图,高度图也是一个思路,只是其中每一个像素不是颜色,而是高度值:
如同可见,子类切片的像素大小和父类是一样的,一般都是256*256的切片,但具体到地理范围上则只有父类的四分之一,所以顾名思义是四叉树。这样,从父类到子类放大的过程中,父类的一个像素,在子类中占了4个像素。也就是一个1:4的映射关系。尽管像素都是整数的,但我们在插值的过程中会有一个亚像素的概念。这样,同一个位置,经纬度都是相同的,但在子类和父类中的uv是不一样的,在对子类的遍历中,获取同一个经纬度对应父类uv的位置,进而得知在父类中相邻的四个像素和权重,进而插值获取其高度(颜色),如下是一个示意代码:
function interpolateMeshHeight(){ var fromWest = (longitude - sourceRectangle.west) * (width - 1) / (sourceRectangle.east - sourceRectangle.west); var fromSouth = (latitude - sourceRectangle.south) * (height - 1) / (sourceRectangle.north - sourceRectangle.south); var widthEdge = (skirtHeight > 0) ? width - 1 : width; var westInteger = fromWest | 0; var eastInteger = westInteger + 1; if (eastInteger >= widthEdge) { eastInteger = width - 1; westInteger = width - 2; } var dx = fromWest - westInteger; return southwestHeight + (dX * (northeastHeight - northwestHeight)) + (dY * (northwestHeight - southwestHeight)) }
QuantizedMeshTerrainData.prototype.upsample
高度图毕竟还都是离散的点值,并没有构网,因而节点之间还没有建立关联,差值算法也相对容易一些。而STK的数据,本身已经是TIN的三角网结构了。这时,在父类中切割出四分之一来就有点复杂了。再打个比方,如果高度图相当于一个棋盘上均匀的大米,然后你四等分,取走其中的一份,而TIN三角网则相当于一个错综复杂的下水管,你要切走四分之一。这要怎么做到呢。假设此时我们有一把利刃,把这个TIN网格横一刀竖一刀,这时,我们迅速的把漏水的管道密封(形成新的节点),这样就实现了TIN三角网重采样的过程。
当然,这个过程相比高度图要复杂的多,因此Cesium中创建了Worker线程,切割的过程都是在线程中完成。具体到算法则如下:
for (i = 0; i < parentIndices.length; i += 3) { var i0 = parentIndices[i]; var i1 = parentIndices[i + 1]; var i2 = parentIndices[i + 2]; var u0 = parentUBuffer[i0]; var u1 = parentUBuffer[i1]; var u2 = parentUBuffer[i2]; triangleVertices[0].initializeIndexed(parentUBuffer, parentVBuffer, parentHeightBuffer, parentNormalBuffer, i0); triangleVertices[1].initializeIndexed(parentUBuffer, parentVBuffer, parentHeightBuffer, parentNormalBuffer, i1); triangleVertices[2].initializeIndexed(parentUBuffer, parentVBuffer, parentHeightBuffer, parentNormalBuffer, i2); // Clip triangle on the east-west boundary. var clipped = Intersections2D.clipTriangleAtAxisAlignedThreshold(halfMaxShort, isEastChild, u0, u1, u2, clipScratch); // Get the first clipped triangle, if any. clippedIndex = 0; if (clippedIndex >= clipped.length) { continue; } clippedIndex = clippedTriangleVertices[0].initializeFromClipResult(clipped, clippedIndex, triangleVertices); if (clippedIndex >= clipped.length) { continue; } clippedIndex = clippedTriangleVertices[1].initializeFromClipResult(clipped, clippedIndex, triangleVertices); if (clippedIndex >= clipped.length) { continue; } clippedIndex = clippedTriangleVertices[2].initializeFromClipResult(clipped, clippedIndex, triangleVertices); // Clip the triangle against the North-south boundary. clipped2 = Intersections2D.clipTriangleAtAxisAlignedThreshold(halfMaxShort, isNorthChild, clippedTriangleVertices[0].getV(), clippedTriangleVertices[1].getV(), clippedTriangleVertices[2].getV(), clipScratch2); if(clipped2.length == 10 && clipped.length == 10) var i = 10; addClippedPolygon(uBuffer, vBuffer, heightBuffer, normalBuffer, indices, vertexMap, clipped2, clippedTriangleVertices, hasVertexNormals); // If there's another vertex in the original clipped result, // it forms a second triangle. Clip it as well. if (clippedIndex < clipped.length) { clippedTriangleVertices[2].clone(clippedTriangleVertices[1]); clippedTriangleVertices[2].initializeFromClipResult(clipped, clippedIndex, triangleVertices); clipped2 = Intersections2D.clipTriangleAtAxisAlignedThreshold(halfMaxShort, isNorthChild, clippedTriangleVertices[0].getV(), clippedTriangleVertices[1].getV(), clippedTriangleVertices[2].getV(), clipScratch2); addClippedPolygon(uBuffer, vBuffer, heightBuffer, normalBuffer, indices, vertexMap, clipped2, clippedTriangleVertices, hasVertexNormals); } }
这个算法有点复杂,但思路清楚了,也就迎刃而解。首先,遍历顶点索引,每次+3,因为三个点构成一个三角形,所以完成了对所有三角网遍历切割的过程。在每次循环中,u0,u1,u2是三角形对应的三个点,然后通过Intersections2D.clipTriangleAtAxisAlignedThreshold实现三角形的切割算法。
这个切割的过程其实就是三角形和直线求交的过程,但更直观一些,因为这个直线是竖直或水平的,如果直线和三角形没有交点,那表示该三角形要么全在子类,要么全不在,不需要切割,我们不讨论这种情况。如果相交,则有两种情况:
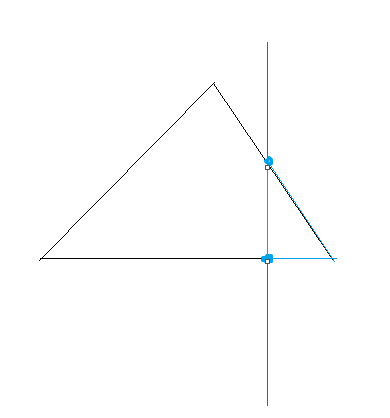
第一种情况,只保留了原三角形一个顶点,但会产生两个新的节点(蓝色),最终形成一个三角形。针对这种情况,我们在做一次水平的切合(水平线和蓝色三角形的相交计算),这个算法是一致的。
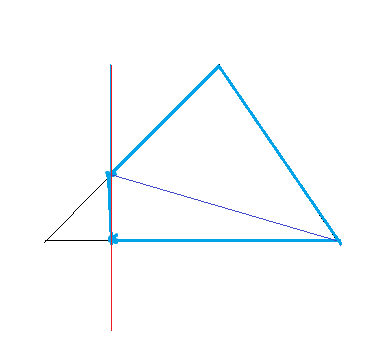
第二种情况,保留了原三角形两个顶点,同时也产生了两个新的节点(必然是偶数节点,哥尼斯堡七桥问题),这时,会形成两个三角形,则我们需要对这两个三角形单独做一次水平切割。
经过如上的逻辑,我们就完成了一个三角形的两刀切,当然,算法只提供了一个思路,并没有考虑特殊情况,正好经过顶点对半切,这个在实际中需要做一次额外的判断,避免少算或重复算。细的说里面有两个过程,求交点,构造新的三角形,分别通过clipTriangleAtAxisAlignedThreshold和addClippedPolygon函数实现。这时,如是是第二种情况,则还有一个三角形需要进行水平的切割和构造新三角形的过程。这是为什么会多一个if判断。
如上,新的,经过重采样的TIN三角网构建完成,Cesium会先渲染这个略微粗糙的地形,等待精细的地形下载完后在更新。当然,通过这个过程,我们能意识到,Cesium并不硬性的要求每一个地形Tile都能够获取到,如果其中一个Tile没有下载到(网络异常或环境限制),也能很好的自适应,而且也不方案该Tile的子类也可以正常渲染和更新。但前提是,根节点的地形数据是必须的。不管是蛋生鸡还是鸡生蛋,你总得现有一样。