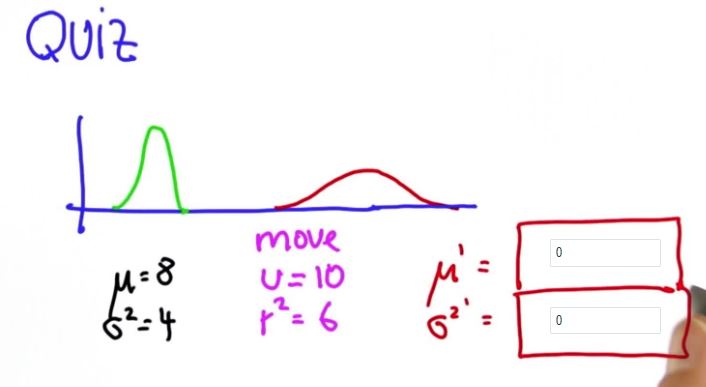
回顾一下之前的内容,我们知道有一个测量更新和一个运动更新(预测)。
运动更新通过全概率或者一个加法来完成,我们已经解决了比较复杂的情况。
我把它解决了 ,并得出了公式。
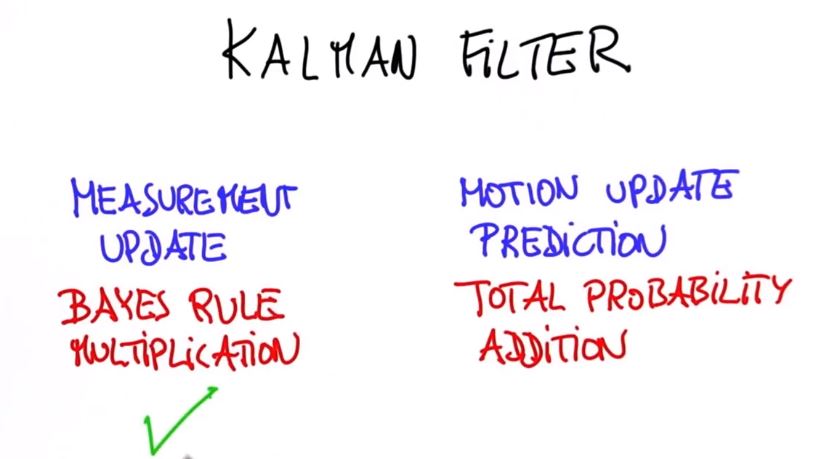
并且也用代码实现了这一步。

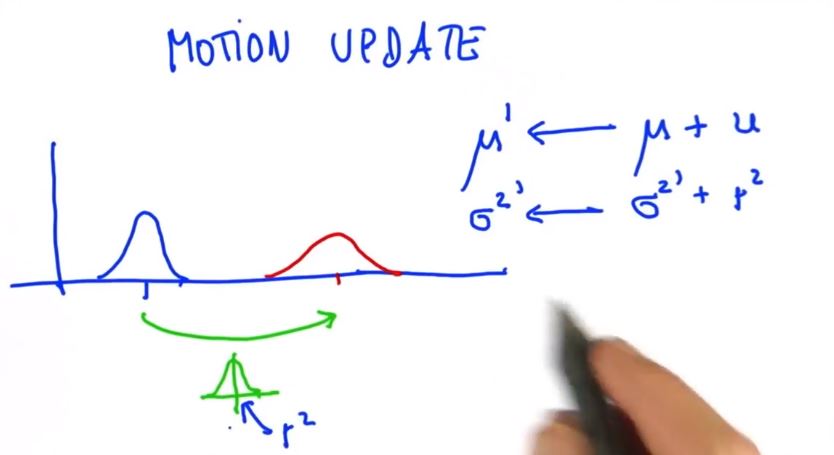
运动部分不想深入,这是非常简单的一步,让我们写下来。假设你活在这样一个世界里,中心点,这是你对自己所在位置的最佳估计,高斯函数是你的误差。
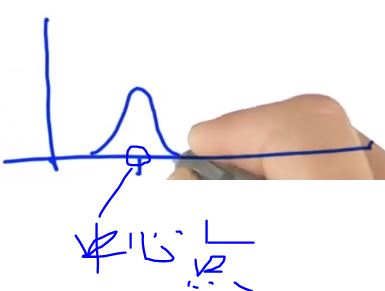
假设你往右移动了一定距离,并且运动本身也包含自己的误差,那么你就到达一个将运动量加到均值上的预测位置,并且这还会在初始误差上增加一个误差。

如果你往右移动了这段距离(绿色线),在期望上你是到达了你想到的地方,但你会丢失信息,因为你的移动本来就会丢失信息,表现在这里的误差上。

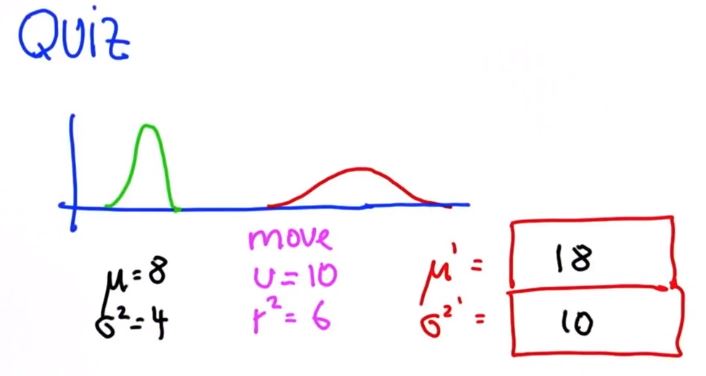
这个在数学上很容易实现,新的平均值等于旧的平均值加上动作,常称为U.
假设你运动了10米 这里将是绿色线将是10米,新的sigma平方等于旧的sigma的平方加上运动的高斯分布方差。
这就是你所需知道的,这不过是一个相加。
测试: