卡尔曼滤波——19.卡尔曼滤波器代码

我们写一个主程序，包括两个函数更新函数和预测函数，然后导入一系列测量和运动数据。

如果初始估计是5，非常好，但我们将其设置为mu=0，且不确定性非常高为sig=10000.

我们假设测量不确定性为常量4，运动不确定性为2.

运动时 你的第一次位置估计应该是4.9.原因在于初始不确定性高，第一次测量值5主导了估计结果。

你的不确定性缩减到了3，99

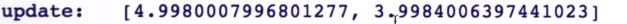
比测量不确定性稍好一点。

然后你的预测加1，但是不确定性增加到了5.99

也就是运动不确定性等于2，然后根据测量数据6 再次跟新 得到你的估计5.99

你再移动1 测量数据为7 你移动2 测量数据9 你移动1  测量数据10 最后移动1.

最后结果出来 该位置的预测为10.99

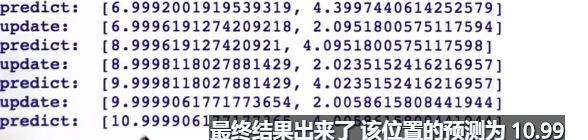
即你的位置10移动1  残留不确定性为4.

# Write a program that will iteratively update and
# predict based on the location measurements 
# and inferred motions shown below. 

def update(mean1, var1, mean2, var2):
    new_mean = float(var2 * mean1 + var1 * mean2) / (var1 + var2)
    new_var = 1./(1./var1 + 1./var2)
    return [new_mean, new_var]

def predict(mean1, var1, mean2, var2):
    new_mean = mean1 + mean2
    new_var = var1 + var2
    return [new_mean, new_var]

measurements = [5., 6., 7., 9., 10.]
motion = [1., 1., 2., 1., 1.]
measurement_sig = 4.
motion_sig = 2.
mu = 0.
sig = 10000.

#Please print out ONLY the final values of the mean
#and the variance in a list [mu, sig]. 

# Insert code here
for n in range(len(measurements)):
    [mu,sig]=update(mu,sig,measurements[n],measurement_sig)
    print 'update:',[mu,sig]
    [mu,sig]=predict(mu,sig,motion[n],motion_sig)
    print 'predict:',[mu,sig]

print [mu, sig]

这段代码部署了整个卡尔曼滤波器，它检查了所有测量元素 并默认，测量值的个数为运动的n次幂，它使用update 递归公式更新mu和sigma.  如果我们导入第n个测量值和测量不确定性，他会对运动进行同样的操作，这里的预测部分，它使用第n个运动和运动不确定性递归地更新mu和sigma 并把这些全部打印出来。

以上就是一个完整的一维卡尔曼滤波。