转自:穆晨
前言
支持向量机,也即SVM,号称分类算法,甚至机器学习界老大哥。其理论优美,发展相对完善,是非常受到推崇的算法。
本文将讲解的SVM基于一种最流行的实现 - 序列最小优化,也即SMO。
另外还将讲解将SVM扩展到非线性可分的数据集上的大致方法。
预备术语
1. 分割超平面:就是决策边界
2. 间隔:样本点到分割超平面的距离
3. 支持向量:离分割超平面距离最近的样本点
算法原理
在前一篇文章 - 逻辑回归中,讲到了通过拟合直线来进行分类。
而拟合的中心思路是求错误估计函数取得最小值,得到的拟合直线是到各样本点距离和最小的那条直线。
然而,这样的做法很多时候未必是最合适的。
请看下图:
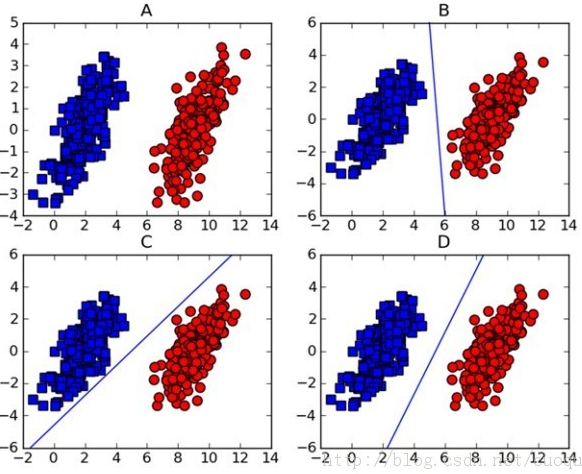
一般来说,逻辑回归得到的直线线段会是B或者C这样的形式。而很显然,从分类算法的健壮性来说,D才是最佳的拟合线段。
SVM分类算法就是基于此思想:找到具有最小间隔的样本点,然后拟合出一个到这些样本点距离和最大的线段/平面。
如何计算最优超平面
1. 首先根据算法思想 - "找到具有最小间隔的样本点,然后拟合出一个到这些样本点距离和最大的线段/平面。" 写出目标函数:

该式子的解就是待求的回归系数。
然而,这是一个嵌套优化问题,非常难进行直接优化求解。为了解这个式子,还需要以下步骤。
2. 不去计算内层的min优化,而是将距离值界定到一个范围 - 大于1,即最近的样本点,也即支持向量到超平面的距离为1。下图可以清楚表示这个意思:

去掉min操作,代之以界定:label * (wTx + b) >= 1。
3. 这样得到的式子就是一个带不等式的优化问题,可以采用拉格朗日乘子法(KKT条件)去求解。
具体步骤推论本文不给出。推导结果为:

另外,可加入松弛系数 C,用于控制 "最大化间隔" 和"保证大部分点的函数间隔小于1.0" 这两个目标的权重。
将 α >= 0 条件改为 C >= α >= 0 即可。
α 是用于求解过程中的一个向量,它和要求的结果回归系数是一一对应的关系。
将其中的 α 解出后,便可依据如下两式子(均为推导过程中出现的式子)进行转换得到回归系数:
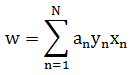
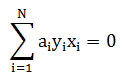
说明: 要透彻理解完整的数学推导过程需要一些时间,可参考某位大牛的文章http://blog.csdn.net/v_july_v/article/details/7624837。
使用SMO - 高效优化算法求解 α 值
算法思想:
每次循环中选择两个 α 进行优化处理。一旦找到一对合适的 α,那么就增大其中一个减小另外一个。
所谓合适,是指必须符合两个条件:1. 两个 α 值必须要在 α 分隔边界之外 2. 这两个α 还没有进行过区间化处理或者不在边界上。
使用SMO求解 α 伪代码:
1 创建一个 alpha 向量并将其初始化为全0 2 当迭代次数小于最大迭代次数(外循环): 3 对数据集中的每个向量(内循环): 4 如果该数据向量可以被优化 5 随机选择另外一个数据向量 6 同时优化这两个向量 7 如果都不能被优化,推出内循环。 8 如果所有向量都没有被优化,则增加迭代数目,继续下一次的循环。
实现及测试代码:
1 #!/usr/bin/env python
2 # -*- coding:UTF-8 -*-
3
4 '''
5 Created on 20**-**-**
6
7 @author: fangmeng
8 '''
9
10 from numpy import *
11 from time import sleep
12
13 #=====================================
14 # 输入:
15 # fileName: 数据文件
16 # 输出:
17 # dataMat: 测试数据集
18 # labelMat: 测试分类标签集
19 #=====================================
20 def loadDataSet(fileName):
21 '载入数据'
22
23 dataMat = []; labelMat = []
24 fr = open(fileName)
25 for line in fr.readlines():
26 lineArr = line.strip().split(' ')
27 dataMat.append([float(lineArr[0]), float(lineArr[1])])
28 labelMat.append(float(lineArr[2]))
29 return dataMat,labelMat
30
31 #=====================================
32 # 输入:
33 # i: 返回结果不等于该参数
34 # m: 指定随机范围的参数
35 # 输出:
36 # j: 0-m内不等于i的一个随机数
37 #=====================================
38 def selectJrand(i,m):
39 '随机取数'
40
41 j=i
42 while (j==i):
43 j = int(random.uniform(0,m))
44 return j
45
46 #=====================================
47 # 输入:
48 # aj: 数据对象
49 # H: 数据对象最大值
50 # L: 数据对象最小值
51 # 输出:
52 # aj: 定界后的数据对象。最大H 最小L
53 #=====================================
54 def clipAlpha(aj,H,L):
55 '为aj定界'
56
57 if aj > H:
58 aj = H
59 if L > aj:
60 aj = L
61 return aj
62
63 #=====================================
64 # 输入:
65 # dataMatIn: 数据集
66 # classLabels: 分类标签集
67 # C: 松弛参数
68 # toler: 荣错率
69 # maxIter: 最大循环次数
70 # 输出:
71 # b: 偏移
72 # alphas: 拉格朗日对偶因子
73 #=====================================
74 def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
75 'SMO算法求解alpha'
76
77 # 数据格式转化
78 dataMatrix = mat(dataMatIn);
79 labelMat = mat(classLabels).transpose()
80 m,n = shape(dataMatrix)
81 alphas = mat(zeros((m,1)))
82
83
84 iter = 0
85 b = 0
86 while (iter < maxIter):
87 # alpha 改变标记
88 alphaPairsChanged = 0
89
90 # 对所有数据集
91 for i in range(m):
92 # 预测结果
93 fXi = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b
94 # 预测结果与实际的差值
95 Ei = fXi - float(labelMat[i])
96 # 如果差值太大则进行优化
97 if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
98 # 随机选择另外一个样本
99 j = selectJrand(i,m)
100 # 计算另外一个样本的预测结果以及差值
101 fXj = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b
102 Ej = fXj - float(labelMat[j])
103 # 暂存当前alpha值对
104 alphaIold = alphas[i].copy();
105 alphaJold = alphas[j].copy();
106 # 确定alpha的最大最小值
107 if (labelMat[i] != labelMat[j]):
108 L = max(0, alphas[j] - alphas[i])
109 H = min(C, C + alphas[j] - alphas[i])
110 else:
111 L = max(0, alphas[j] + alphas[i] - C)
112 H = min(C, alphas[j] + alphas[i])
113 if L==H:
114 pass
115 # eta为alphas[j]的最优修改量
116 eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T
117 if eta >= 0:
118 print "eta>=0"; continue
119 # 订正alphas[j]
120 alphas[j] -= labelMat[j]*(Ei - Ej)/eta
121 alphas[j] = clipAlpha(alphas[j],H,L)
122 # 如果alphas[j]发生了轻微变化
123 if (abs(alphas[j] - alphaJold) < 0.00001):
124 continue
125 # 订正alphas[i]
126 alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])
127
128 # 订正b
129 b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
130 b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
131 if (0 < alphas[i]) and (C > alphas[i]): b = b1
132 elif (0 < alphas[j]) and (C > alphas[j]): b = b2
133 else: b = (b1 + b2)/2.0
134
135 # 更新修改标记参数
136 alphaPairsChanged += 1
137
138 if (alphaPairsChanged == 0): iter += 1
139 else: iter = 0
140
141 return b,alphas
142
143 def test():
144 '测试'
145
146 dataArr, labelArr = loadDataSet('/home/fangmeng/testSet.txt')
147 b, alphas = smoSimple(dataArr, labelArr, 0.6, 0.001, 40)
148 print b
149 print alphas[alphas>0]
150
151
152 if __name__ == '__main__':
153 test()
其中,testSet.txt数据文件格式为三列,前两列特征,最后一列分类结果。
测试结果:

结果具有随机性,多次运行的结果不一定一致。
得到 alphas 数组和 b 向量就能直接算到回归系数了,参考上述代码 93 行,稍作变换即可。
非线性可分情况的大致解决思路
当数据分析图类似如下的情况:
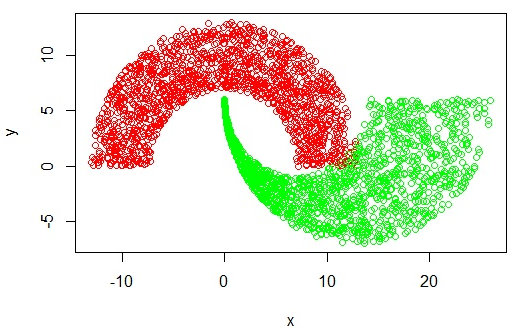
则显然无法拟合出一条直线来。碰到这种情况的解决办法是使用核函数 - 将在低维处理非线性问题转换为在高维处理线性问题。
也就是说,将在SMO中所有出现了向量内积的地方都替换成核函数处理。
具体的用法,代码本文不做讲解。
小结
支持向量机是分类算法中目前用的最多的,也是最为完善的。
关于支持向量机的讨论远远不会止于此,本文初衷仅仅是对这个算法有一定的了解,认识。
若是在以后的工作中需要用到这方面的知识,还需要全面深入的学习,研究。
